题目内容
已知等差数列 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
(1)求通项公式
(2)设 ,求数列
,求数列 的前
的前 项和
项和
【答案】
(1) ;(2)
;(2) 或
或 。
。
【解析】
试题分析:⑴由题意知

所以 (6分)
(6分)
⑵当 时,数列
时,数列 是首项为
是首项为 、公比为8的等比数列
、公比为8的等比数列
所以
当 时,
时, 所以
所以
综上,所以 或
或 (12分)
(12分)
考点:等差数列的简单性质;等比数列的简单性质;等差数列的通项公式和前n项和公式;等比数列的通项公式和前n项和公式。
点评:本题主要考查等差数列和等比数列的基本运算。通过列方程(组)所有问题可迎刃而解,解决此类问题的关键是熟练掌握等差和等比的有关公式,并灵活应用,在运算过程中,还应善于应用整体代换思想简化运算的过程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
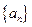 的前四项和为10,且
的前四项和为10,且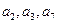 成等比数列。
成等比数列。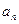 ; (2)设
; (2)设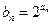 ,求数列
,求数列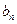 的前
的前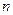 项和
项和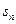
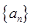 的前四项和为10,且
的前四项和为10,且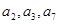 成等比数列
成等比数列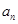
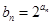 ,求数列
,求数列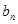 的前
的前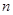 项和
项和 。
。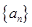 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
 ,求数列
,求数列 的前
的前 项和
项和
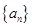 的前四项和为10,且
的前四项和为10,且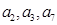 成等比数列
成等比数列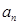 ,
,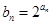 ,求数列
,求数列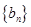 的前
的前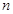 项和
项和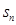 。
。