题目内容
已知函数 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有 ,且满足
,且满足 .
.
(1)求 的值;
的值;
(2)求满足 的
的 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:
解题思路:(1)将 进行赋值求解即可;(2)将
进行赋值求解即可;(2)将 变形为
变形为 ,利用函数的单调性解不等式.
,利用函数的单调性解不等式.
规律总结:解决抽象函数的求值、证明等问题,要灵活利用其结构特点进行恰当赋值;解不等式时,要将所求不等式化成 的形式,则利用函数的单调性进行化简求解.
的形式,则利用函数的单调性进行化简求解.
试题解析:(1)取 ,得
,得 , 则
, 则 ,
,
取 ,得
,得 , 则
, 则
(2)由题意得, ,故
,故 ,解得
,解得  .
.
考点:抽象函数.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 .
. 的单调区间;
的单调区间; 在
在 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值; ,证明:
,证明: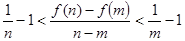
 (
( 为常数,
为常数, 且
且 )的图象过点
)的图象过点 .
. ,试判断函数
,试判断函数 的奇偶性,并说明理由
的奇偶性,并说明理由 .
. 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围; ,若函数
,若函数 在 [1,3]上恰有两个不同零点,求实数
在 [1,3]上恰有两个不同零点,求实数 的取值范围.
的取值范围. 则
则 有三个根;
有三个根; ;
; 与直线
与直线 平行的充要条件是
平行的充要条件是
 的定义域是
的定义域是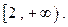
 的图象关于原点对称,则
的图象关于原点对称,则 ________________.
________________.
 满足
满足 ,且在区间
,且在区间 上是增函数,若方程f(x)=m(m>0)在区间
上是增函数,若方程f(x)=m(m>0)在区间 上有四个不同的根,则
上有四个不同的根,则
 的定义域为 .
的定义域为 .