题目内容
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若 在
在 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值;
(3)对任意的 ,证明:
,证明: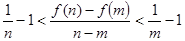
(1) 递增区间为
递增区间为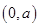 ,递减区间为
,递减区间为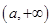 ;(2)
;(2) ;(3)略.
;(3)略.
解析试题分析:此题是导数的综合题.(1)考察函数的求导,导数大于(大于或等于)零的区间即为函数递增区间,小于(小于或等于)零的区间即为函数递减区间;(2)恒成立问题一般情况下是转化为求最值问题,借助第一问的单调性,注意主元思想的变换;(3)见详解.
试题解析:(1) ,
,
当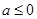 时,
时,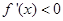 ,
, 减区间为
减区间为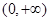
当 时,由
时,由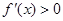 得
得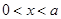 ,由
,由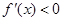 得
得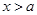
∴ 递增区间为
递增区间为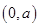 ,递减区间为
,递减区间为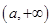
(2)由(1)知:当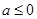 时,
时, 在
在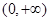 上为减区间,而
上为减区间,而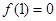
∴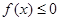 在区间
在区间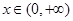 上不可能恒成立
上不可能恒成立
当 时,
时, 在
在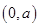 上递增,在
上递增,在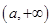 上递减,
上递减,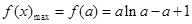 ,令
,令 , 依题意有
, 依题意有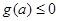 ,而
,而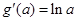 ,且
,且
∴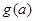 在
在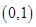 上递减,在
上递减,在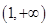 上递增,∴
上递增,∴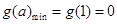 ,故
,故
(3)由(2)知: 时,
时,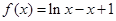 且
且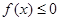 恒成立
恒成立
即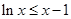 恒成立则
恒成立则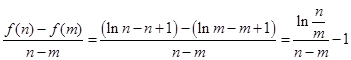
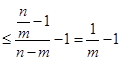 又由
又由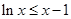 知
知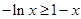 在
在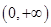 上恒成立,
上恒成立,
∴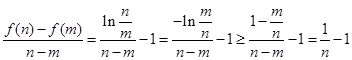
综上所述:对任意的 ,证明:
,证明: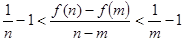
考点:导数的求法,利用导数求函数最值,不等式的证明.

练习册系列答案
相关题目
 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有 ,且满足
,且满足 .
. 的值;
的值;  的
的 的取值范围.
的取值范围.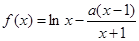 (
(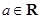 ,
,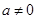 ),
),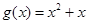 .
.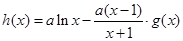 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数; (
( ).
). .
. 的定义域;
的定义域;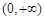 上的三个函数
上的三个函数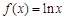 ,
,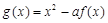 ,
,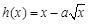 ,且
,且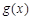 在
在 处取得极值.
处取得极值.

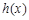 的单调区间.
的单调区间.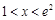 时,恒有
时,恒有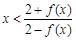 成立.[来源
成立.[来源 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
, ,且
,且 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一直线交
作一直线交 于
于 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设 .
. 表示为
表示为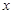 的函数;
的函数; 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.
 满足
满足 ,则
,则 的值为 .
的值为 .  的定义域为
的定义域为 ,集合
,集合 ,若P:“
,若P:“ ”是
”是 ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围 .
的取值范围 . ,
, ,
, ,
, ,
, ,
, 为报刊零售点.请确定一个格点(除零售点外)__________为发行站,使6个零售点沿街道到发行站之间路程的和最短.
为报刊零售点.请确定一个格点(除零售点外)__________为发行站,使6个零售点沿街道到发行站之间路程的和最短.