题目内容
非零向量(a+b)与(2a-b)互相垂直，(a-2b)与(2a+b)垂直，求向量a与b的夹角.
解：∵(a+b)⊥(2a-b),
同时(a-2b)⊥(2a+b),
∴
∴
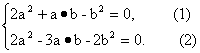
①×3+②，得a2=
b2,∴|a|2=
|b|2.
由①得a·b=b2-2a2=|b|2-2×
|b|2
=-
|b|2.
∴cosθ=
=
=-
×
.
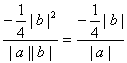
∴cosθ=-
.
∵0°≤θ≤180°,∴θ=arccos(-
)，
即θ=180°-arccos
.
练习册系列答案
计算高手系列答案
相关题目
+
=
+
.正确命题的个数是( ) 
是“a与b共线”的