题目内容
已知函数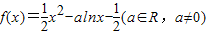 .
.(Ⅰ)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若对任意的x∈[1,+∞),都有f(x)≥0成立,求a的取值范围.
【答案】分析:(I)当a=2时,写出f(x)的表达式,对f(x)进行求导,求出x=1处的斜率,再根据点斜式求出切线的方程;
(II)求出函数的定义域,令f′(x)大于0求出x的范围即为函数的增区间;令f′(x)小于0求出x的范围即为函数的减区间;
(III)由题意可知,对任意的x∈[1,+∞),使f(x)≥0成立,只需任意的x∈[1,+∞),f(x)min≥0.下面对a进行分类讨论,从而求出a的取值范围;
解答:解:(Ⅰ)a=2时,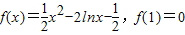 …(1分)
…(1分)
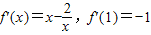 …(2分)
…(2分)
曲线y=f(x)在点(1,f(1))处的切线方程x+y-1=0…(3分)
(Ⅱ)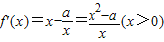 …(4分)
…(4分)
①当a<0时,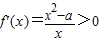 恒成立,函数f(x)的递增区间为(0,+∞)
恒成立,函数f(x)的递增区间为(0,+∞)
…(6分)
②当a>0时,令f'(x)=0,解得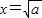 或
或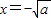
所以函数f(x)的递增区间为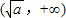 ,递减区间为
,递减区间为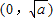
…(8分)
(Ⅲ)对任意的x∈[1,+∞),使f(x)≥0成立,只需任意的x∈[1,+∞),f(x)min≥0
①当a<0时,f(x)在[1,+∞)上是增函数,
所以只需f(1)≥0
而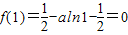
所以a<0满足题意; …(9分)
②当0<a≤1时,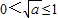 ,f(x)在[1,+∞)上是增函数,
,f(x)在[1,+∞)上是增函数,
所以只需f(1)≥0
而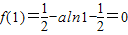
所以0<a≤1满足题意;…(10分)
③当a>1时,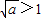 ,f(x)在
,f(x)在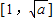 上是减函数,
上是减函数,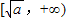 上是增函数,
上是增函数,
所以只需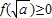 即可
即可
而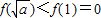
从而a>1不满足题意; …(12分)
综合①②③实数a的取值范围为(-∞,0)∪(0,1].…(13分)
点评:考查利用导数研究曲线上某点切线方程、利用导数研究函数的极值和单调性.恒成立的问题,一般都要求函数的最值,此题是一道中档题.
(II)求出函数的定义域,令f′(x)大于0求出x的范围即为函数的增区间;令f′(x)小于0求出x的范围即为函数的减区间;
(III)由题意可知,对任意的x∈[1,+∞),使f(x)≥0成立,只需任意的x∈[1,+∞),f(x)min≥0.下面对a进行分类讨论,从而求出a的取值范围;
解答:解:(Ⅰ)a=2时,
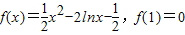 …(1分)
…(1分)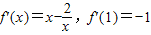 …(2分)
…(2分)曲线y=f(x)在点(1,f(1))处的切线方程x+y-1=0…(3分)
(Ⅱ)
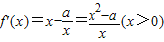 …(4分)
…(4分)①当a<0时,
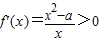 恒成立,函数f(x)的递增区间为(0,+∞)
恒成立,函数f(x)的递增区间为(0,+∞)…(6分)
②当a>0时,令f'(x)=0,解得
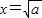 或
或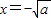
| x | ( 0, ) ) | 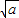 | ( 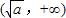 ,1) ,1) |
| f′(x) | - | + | |
| f(x) | 减 | 增 |
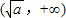 ,递减区间为
,递减区间为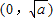
…(8分)
(Ⅲ)对任意的x∈[1,+∞),使f(x)≥0成立,只需任意的x∈[1,+∞),f(x)min≥0
①当a<0时,f(x)在[1,+∞)上是增函数,
所以只需f(1)≥0
而
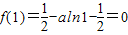
所以a<0满足题意; …(9分)
②当0<a≤1时,
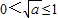 ,f(x)在[1,+∞)上是增函数,
,f(x)在[1,+∞)上是增函数,所以只需f(1)≥0
而
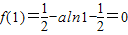
所以0<a≤1满足题意;…(10分)
③当a>1时,
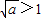 ,f(x)在
,f(x)在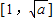 上是减函数,
上是减函数,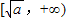 上是增函数,
上是增函数,所以只需
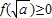 即可
即可而
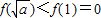
从而a>1不满足题意; …(12分)
综合①②③实数a的取值范围为(-∞,0)∪(0,1].…(13分)
点评:考查利用导数研究曲线上某点切线方程、利用导数研究函数的极值和单调性.恒成立的问题,一般都要求函数的最值,此题是一道中档题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
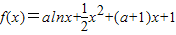 .
. .
. .
.