Question

已知F₁(-c,0)、F₂(c,0)是离心率为的椭圆的两个焦点,A为椭圆的一个短轴端点,且·=-1.

(1)求椭圆方程;

(2)过点P(0,2)的直线交椭圆于C、D两点,求的取值范围.

Answer 1

解:(1)设椭圆方程为=1(a＞b＞0),

由e==得a²=3b².

故椭圆方程为x²+3y²=3b².

F₁(,0)、F₂(,0)、A(0,b),

=(,-b)，=（,-b）,

·=-2b²+b²=-b²=-1.

∴b²=1.

∴椭圆方程为x²+3y²=3.

(2)设=λ,显然λ≠1,由于与同向,故=λ.

设C(x₀,y₀)、D(m,n),则(x₀,y₀-2)=λ(m,n-2),

∴

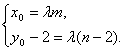
由C、D在椭圆x²+3y²=3上

得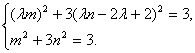

消去m得4λ(λ-1)n=(5λ-3)(λ-1),n=.

又∵|n|≤1,∴||≤1,解得≤λ≤3.

故的取值范围是［,1)∪(1,3].