题目内容
已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)是否存在实数![]() ,使得
,使得![]() 在
在![]() 处取极值?证明你的结论;
处取极值?证明你的结论;
(Ⅱ)若![]() 在[-1,
在[-1,![]() ]上是增函数,求实数
]上是增函数,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)f ′(x) = ax2 – ax + 1
假设存在实数a,使f (x)在x =![]() 处取极值,则
处取极值,则
f ′(![]() ) = –
) = –![]() + 1 = 0, ∴a = 4 --------------------------------------------------- 3分
+ 1 = 0, ∴a = 4 --------------------------------------------------- 3分
此时,f ′(x) =![]()
当x <![]() 时,f ′(x) > 0;当
时,f ′(x) > 0;当![]() <x<1时,f ′(x) > 0.
<x<1时,f ′(x) > 0.
∴x =![]() 不是f (x)的极值点,
不是f (x)的极值点,
故不存在实数a,使f (x)在x =![]() 处极值 -------------------------------- 6分
处极值 -------------------------------- 6分
(Ⅱ)依题意知:当x∈[-1,![]() ]时,f ′(x) = ax2 – ax + 1≥0恒成立,
]时,f ′(x) = ax2 – ax + 1≥0恒成立,
(1)当a = 0时,f ′(x) = 1>0成立;
(2)当a>0时,f ′(x) = a (x![]() )2 + 1
)2 + 1![]() 在
在![]() 上递减,则
上递减,则
g (x)min = g (![]() ) = 1
) = 1![]() ≥0 ∴0<a≤4 ----------------------------------9分
≥0 ∴0<a≤4 ----------------------------------9分
(3)当a<0时,f ′(x) = a (x![]() )2 + 1
)2 + 1![]() 在
在![]() 上递增,则
上递增,则
g (x)min = g (-1) = 2a + 1≥0 ∴0>a≥![]()
综上,![]() ≤a≤4为所求 -------------------------------------------------- 12分
≤a≤4为所求 -------------------------------------------------- 12分

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目






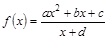 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.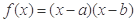 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
