Question

【题目】已知函数，

（1）试证明函数是偶函数；

（2）画出的图象；（要求先用铅笔画出草图，再用黑色签字笔描摹，否则不给分）

（3）请根据图象指出函数的单调递增区间与单调递减区间；（不必证明）

（4）当实数取不同的值时，讨论关于的方程的实根的个数；（不必求出方程的解）

Answer 1

【答案】（1）详见解析（2）详见解析（3）增区间减区间（4）①当时，方程无实数根；②当或时，方程有两个实数根；③当时，方程有三个实数根；④当时，方程有四个实数根

【解析】

试题分析：（1）根据函数的定义域为R，关于原点对称，且满足f（-x）=f（x），可得函数 f（x）是偶函数.（2）先去绝对值，然后根据二次函数、分段函数图象的画法画出函数f（x）的图象.（3）通过图象即可求得f（x）的单调递增和递减区间；（4）通过图象即可得到k的取值和对应的原方程实根的个数

试题解析：（1）的定义域为,且

故为偶函数；

（2）如图

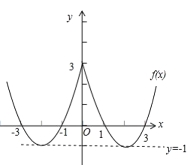
（3）递增区间有：

递减区间有：

（4）根据图象可知，

①当时，方程无实数根；

②当或时，方程有两个实数根；

③当时，方程有三个实数根；

④当时，方程有四个实数根；