题目内容
四个△ABC分别满足下列条件,
(1)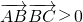 ;
;
(2)tanA•tanB>1;
(3)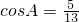 ,
,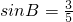 ;
;
(4)sinA+cosA<1
则其中是锐角三角形有
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:根据数量积判断(1)的正误;利用正切化为正弦函数余弦函数以及两角差的三角函数判断三角形的形状;
通过三角函数值判断角的大小,推出三角形的形状;利用三角函数的现在判断(4)的形状;
解答:(1)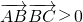 ;
; ,所以∠B是钝角,三角形不是锐角三角形.
,所以∠B是钝角,三角形不是锐角三角形.
(2)tanA•tanB>1;可得A,B是锐角,且sinAsinB>cosAcosB,所以cos(A+B)<0.所以C为锐角,三角形是锐角三角形.
(3)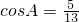
 ,A∈(
,A∈(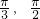 ),
),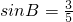 ; B∈(
; B∈( )三角形是锐角三角形.
)三角形是锐角三角形.
(4)sinA+cosA<1,因为sinA+cosA= sin(A+
sin(A+ )<1,A为锐角时
)<1,A为锐角时 sin(A+
sin(A+ )>1,说明A为钝角;
)>1,说明A为钝角;
故选B.
点评:本题是基础题,考查三角形的形状的判断,注意三角函数值的范围与角的范围的确定,向量的数量积的应用.考查判断分析能力.
分析:根据数量积判断(1)的正误;利用正切化为正弦函数余弦函数以及两角差的三角函数判断三角形的形状;
通过三角函数值判断角的大小,推出三角形的形状;利用三角函数的现在判断(4)的形状;
解答:(1)
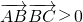 ;
; ,所以∠B是钝角,三角形不是锐角三角形.
,所以∠B是钝角,三角形不是锐角三角形.(2)tanA•tanB>1;可得A,B是锐角,且sinAsinB>cosAcosB,所以cos(A+B)<0.所以C为锐角,三角形是锐角三角形.
(3)
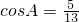
 ,A∈(
,A∈(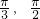 ),
),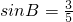 ; B∈(
; B∈( )三角形是锐角三角形.
)三角形是锐角三角形. (4)sinA+cosA<1,因为sinA+cosA=
 sin(A+
sin(A+ )<1,A为锐角时
)<1,A为锐角时 sin(A+
sin(A+ )>1,说明A为钝角;
)>1,说明A为钝角;故选B.
点评:本题是基础题,考查三角形的形状的判断,注意三角函数值的范围与角的范围的确定,向量的数量积的应用.考查判断分析能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
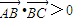 ;
; ,
,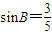 ;
;