题目内容
四个△ABC分别满足下列条件,
(1)
•
>0;
(2)tanA•tanB>1;
(3)cosA=
,sinB=
;
(4)sinA+cosA<1
则其中是锐角三角形有( )
(1)
| AB |
| BC |
(2)tanA•tanB>1;
(3)cosA=
| 5 |
| 13 |
| 3 |
| 5 |
(4)sinA+cosA<1
则其中是锐角三角形有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
(1)
•
>0;
•
= |
•|
cos<
•
>0>0,所以∠B是钝角,三角形不是锐角三角形.
(2)tanA•tanB>1;可得A,B是锐角,且sinAsinB>cosAcosB,所以cos(A+B)<0.所以C为锐角,三角形是锐角三角形.
(3)cosA=
<
,A∈(
,
),sinB=
; B∈(
,
)三角形是锐角三角形.
(4)sinA+cosA<1,因为sinA+cosA=
sin(A+
)<1,A为锐角时
sin(A+
)>1,说明A为钝角;
故选B.
| AB |
| BC |
| AB |
| BC |
| AB |
| BC| |
| AB |
| BC |
(2)tanA•tanB>1;可得A,B是锐角,且sinAsinB>cosAcosB,所以cos(A+B)<0.所以C为锐角,三角形是锐角三角形.
(3)cosA=
| 5 |
| 13 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 3 |
| 5 |
| π |
| 6 |
| π |
| 4 |
(4)sinA+cosA<1,因为sinA+cosA=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
故选B.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
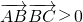 ;
;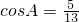 ,
,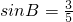 ;
; 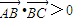 ;
; ,
,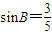 ;
;