题目内容
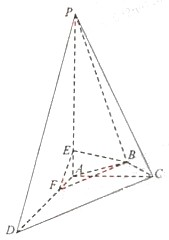
（2012•天津）如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．（1）证明：PC⊥AD；
（2）求二面角A-PC-D的正弦值；
（3）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长．
分析：解法一（1）以A为原点，建立空间直角坐标系，通过得出
•
=0，证出PC⊥AD．
（2）求出平面PCD，平面PCD的一个法向量，利用两法向量夹角求解．
（3）设E（0，0，h），其中h∈[0，2]，利用cos＜
＞=cos30°=
，得出关于h的方程求解即可．
解法二：（1）通过证明AD⊥平面PAC得出PC⊥AD．
（2）作AH⊥PC于点H，连接DH，∠AHD为二面角A-PC-D的平面角．在RT△DAH中求解
（3）因为∠ADC＜45°，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF，故∠EBF（或其补角）为异面直线BE与CD所成的角．在△EBF中，因为EF＜BE，从而∠EBF=30°，由余弦定理得出关于h的方程求解即可．
| PC |
| AD |
（2）求出平面PCD，平面PCD的一个法向量，利用两法向量夹角求解．
（3）设E（0，0，h），其中h∈[0，2]，利用cos＜
| BE |
| ，CD |
| ||
| 2 |
解法二：（1）通过证明AD⊥平面PAC得出PC⊥AD．
（2）作AH⊥PC于点H，连接DH，∠AHD为二面角A-PC-D的平面角．在RT△DAH中求解
（3）因为∠ADC＜45°，故过点B作CD的平行线必与线段AD相交，设交点为F，连接BE，EF，故∠EBF（或其补角）为异面直线BE与CD所成的角．在△EBF中，因为EF＜BE，从而∠EBF=30°，由余弦定理得出关于h的方程求解即可．
解答：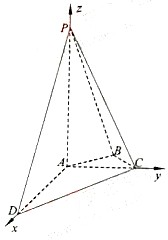
解法一：如图，以A为原点，建立空间直角坐标系，则A（0，0，0），D（2，0，0），C（0，1，0），B（-
，
，0），P（0，0，2）．
（1）证明：易得
=（0，1，-2），
=（2，0，0），于是
•
=0，所以PC⊥AD．
（2）解：
=（0，1，-2），
=（2，-1，0），设平面PCD的一个法向量为
=（x，y，z），则
即
取z=1，则以
=（1，2，1）．又平面PAC的一个法向量为
=（1，0，0），于是cos＜
，
＞=
=
，sin＜
，
＞=
所以二面角A-PC-D的正弦值为
．
（3）设E（0，0，h），其中h∈[0，2]，由此得
=（
，-
，h）．由
=（2，-1，0），故cos＜
＞=
=
=
所以
=cos30°=
，解得h=
，即AE=
．
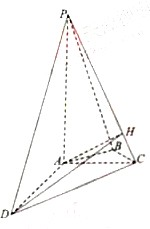
解法二：（1）证明：由PA⊥平面ABCD，可得PA⊥AD，
又由AD⊥AC，PA∩AC=A，故AD⊥平面PAC，
又PC?平面PAC，
所以PC⊥AD．
（2）解：如图，作AH⊥PC于点H，连接DH，
由PC⊥AD，PC⊥AH，可得PC⊥平面ADH，因此DH⊥PC，从而∠AHD为二面角A-PC-D的平面角．
在RT△PAC中，PA=2，AC=1，所以AH=
，由（1）知，AD⊥AH，在RT△DAH中，DH=
=
，因此sin∠AHD=
=
．所以二面角A-PC-D的正弦值为
．
（3）解：如图，因为∠ADC＜45°，故过点B作CD的平行线必与线段AD相交，
设交点为F，连接BE，EF，故∠EBF（或其补角）为异面直线BE与CD所成的角．
由于BF∥CD，故∠AFB=∠ADC，在RT△DAC中，CD=
，sin=∠ADC=
，故sin∠AFB=
．
在△AFB中，由
=
，AB=
，sin∠FAB=sin135°=
，可得BF=
，
由余弦定理，BF2=AB2+AF2-2ABAFcos∠FAB，得出AF=
，
设AE=h，在RT△EAF中，EF=
=
，
在RT△BAE中，BE=
=
，
在△EBF中，因为EF＜BE，从而∠EBF=30°，
由余弦定理得到，cos30°=
，
解得h=
，
即AE=
．
解法一：如图，以A为原点，建立空间直角坐标系，则A（0，0，0），D（2，0，0），C（0，1，0），B（-| 1 |
| 2 |
| 1 |
| 2 |
（1）证明：易得
| PC |
| AD |
| PC |
| AD |
（2）解：
| PC |
| CD |
| n |
|
|
取z=1，则以
| n |
| m |
| m |
| n |
| ||||
|
|
| ||
| 6 |
| m |
| n |
| ||
| 6 |
所以二面角A-PC-D的正弦值为
| ||
| 6 |
（3）设E（0，0，h），其中h∈[0，2]，由此得
| BE |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
| BE |
| ，CD |
| ||||
|
| ||||||
|
| 3 | ||
|
所以
| 3 | ||
|
| ||
| 2 |
| ||
| 10 |
| ||
| 10 |
解法二：（1）证明：由PA⊥平面ABCD，可得PA⊥AD，
又由AD⊥AC，PA∩AC=A，故AD⊥平面PAC，
又PC?平面PAC，
所以PC⊥AD．
（2）解：如图，作AH⊥PC于点H，连接DH，
由PC⊥AD，PC⊥AH，可得PC⊥平面ADH，因此DH⊥PC，从而∠AHD为二面角A-PC-D的平面角．
在RT△PAC中，PA=2，AC=1，所以AH=
| 2 | ||
|
| AD2+AH2 |
2
| ||
| 5 |
| AD |
| DH |
| ||
| 6 |
| ||
| 6 |
（3）解：如图，因为∠ADC＜45°，故过点B作CD的平行线必与线段AD相交，
设交点为F，连接BE，EF，故∠EBF（或其补角）为异面直线BE与CD所成的角．
由于BF∥CD，故∠AFB=∠ADC，在RT△DAC中，CD=
| 5 |
| 1 | ||
|
| 1 | ||
|
在△AFB中，由
| BF |
| sin∠FAB |
| AB |
| sin∠AFB |
| 2 |
| ||
| 2 |
| ||
| 2 |
由余弦定理，BF2=AB2+AF2-2ABAFcos∠FAB，得出AF=
| 1 |
| 2 |
设AE=h，在RT△EAF中，EF=
| AE2+AF2 |
h2+
|
在RT△BAE中，BE=
| AE2+AB2 |
h2+
|
在△EBF中，因为EF＜BE，从而∠EBF=30°，
由余弦定理得到，cos30°=
| BE2+BF2-EF2 |
| 2BE•BF |
解得h=
| ||
| 10 |
即AE=
| ||
| 10 |
点评：本题考查线面关系，直线与直线所成的角、二面角等基础知识，考查思维能力、空间想象能力，并考查应用向量知识解决数学问题能力．
练习册系列答案
相关题目
（2012•天津）如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=
（2012•天津）如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2
，PD＝CD＝2.
，PD＝CD＝2.