题目内容
已知两个不相等的平面向量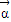 ,
, (
(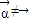 )满足|
)满足|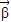 |=2,且
|=2,且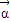 与
与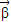 -
-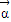 的夹角为120°,则|
的夹角为120°,则|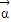 |的最大值是 .
|的最大值是 .
【答案】分析:如图所示:设 =
= ,
, =
= ,则
,则  =
= ,∠BAO=60°,∠BAC=120°,且 OB=2,0°<∠B<120°.△AOB中,由正弦定理求得|
,∠BAO=60°,∠BAC=120°,且 OB=2,0°<∠B<120°.△AOB中,由正弦定理求得| |=
|= sin∠B,由此可得|
sin∠B,由此可得| |的最大值.
|的最大值.
解答: 解:如图所示:设
解:如图所示:设 =
= ,
, =
= ,则
,则  =
= ,∠BAO=60°,∠BAC=120°,
,∠BAO=60°,∠BAC=120°,
且 OB=2,0°<∠B<120°.
△AOB中,由正弦定理可得 =
= ,即
,即  ,
,
解得| |=
|= sin∠B.
sin∠B.
由于当∠B=90°时,sin∠B最大为1,故| |的最大值是
|的最大值是 ,
,
故答案为 .
.
点评:本题主要考查求向量的模的方法,正弦定理,以及正弦函数的值域,体现了数形结合的数学思想,属于中档题.
 =
= ,
, =
= ,则
,则  =
= ,∠BAO=60°,∠BAC=120°,且 OB=2,0°<∠B<120°.△AOB中,由正弦定理求得|
,∠BAO=60°,∠BAC=120°,且 OB=2,0°<∠B<120°.△AOB中,由正弦定理求得| |=
|= sin∠B,由此可得|
sin∠B,由此可得| |的最大值.
|的最大值.解答:
 解:如图所示:设
解:如图所示:设 =
= ,
, =
= ,则
,则  =
= ,∠BAO=60°,∠BAC=120°,
,∠BAO=60°,∠BAC=120°,且 OB=2,0°<∠B<120°.
△AOB中,由正弦定理可得
 =
= ,即
,即  ,
,解得|
 |=
|= sin∠B.
sin∠B.由于当∠B=90°时,sin∠B最大为1,故|
 |的最大值是
|的最大值是 ,
,故答案为
 .
.点评:本题主要考查求向量的模的方法,正弦定理,以及正弦函数的值域,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
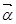 ,
,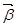 (
(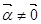 )满足|
)满足|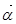 |的最大值是
|的最大值是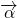 ,
, (
( )满足|
)满足|