题目内容
15．已知函数f（x）=a-x2（1≤x≤2）与g（x）=x+1的图象上存在关于x轴对称的点，则实数a的取值范围是（ ）| A． | $[-\frac{5}{4}，+∞）$ | B． | [1，2] | C． | $[-\frac{5}{4}，1]$ | D． | [-1，1] |
分析 由已知，得到方程a-x2=-（x+1）?a=x2-x-1在区间[1，2]上有解，构造函数g（x）=x2-x-1，求出它的值域，得到a的范围即可
解答 解：若函数f（x）=a-x2（1≤x≤2）与g（x）=x+1的图象上存在关于x轴对称的点，
则方程a-x2=-（x+1）?a=x2-x-1在区间[1，2]上有解，
令g（x）=x2-x-1，1≤x≤2，
由g（x）=x2-x-1的图象是开口朝上，且以直线x=$\frac{1}{2}$为对称轴的抛物线，
故当x=1时，g（x）取最小值-1，当x=2时，函数取最大值1，
故a∈[-1，1]，
故选：D
点评 本题考查了构造函数法求方程的解及参数范围；关键是将已知转化为方程a=x2-x-1在区间[1，2]上有解．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
6．已知函数f（x）=$\sqrt{3}$sinωx+cosωx（其中ω＞0）的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列，把函数f（x）的图象沿x轴向左平移$\frac{π}{6}$个单位得到函数g（x）的图象，则g（x）的单调递减区间是（ ）
| A． | [kπ，$\frac{π}{2}$+kπ]，k∈Z | B． | [-$\frac{π}{2}$+kπ，kπ]，k∈Z | ||
| C． | [-$\frac{π}{4}$+kπ，$\frac{π}{4}$+kπ]，k∈Z | D． | [$\frac{π}{4}$+kπ，$\frac{3π}{4}$+kπ]，k∈Z |
10．已知向量$\overrightarrow{a}=（sinθ，cosθ）$，$\overrightarrow{b}$=（3，4），若$\overrightarrow{a}⊥\overrightarrow{b}$，则tanθ等于（ ）
| A． | $-\frac{24}{7}$ | B． | $\frac{6}{7}$ | C． | $-\frac{24}{25}$ | D． | $-\frac{4}{3}$ |
20．在正方体ABCD-A1B1C1D1中，异面直线AC与BC1所成角的大小是（ ）
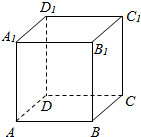
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
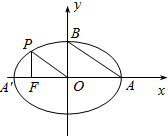如图，A，A′，B分别是椭圆顶点，从椭圆上一点P向x轴作垂线，垂足为左焦点F，且AB∥OP，则椭圆的离心率为$\frac{\sqrt{2}}{2}$．