题目内容
5.已知一工厂生产某种产品的年固定成本为100万元,每生产1千件需另投入27万元.设该工厂一年内生产这种产品x千件并全部销售完,每千件的销售收入为p(x)万元,且$p(x)=\left\{\begin{array}{l}108-\frac{1}{3}{x^2},0<x≤10\\ \frac{1080}{x}-\frac{10000}{{3{x^2}}},x>10\end{array}\right.$(Ⅰ)写出年利润f(x)(万元)关于年产量x(千件)的函数关系式;
(Ⅱ)年产量为多少千件时,该工厂在这种产品的生产中所获得的年利润最大?
(注:年利润=年销售收入-年总成本)
分析 (Ⅰ)由年利润=年销售收入-年总成本,结合p(x),即可得到所求f(x)的解析式;
(Ⅱ)讨论0<x≤10时,由导数判断单调性,可得最大值;再讨论x>10时,运用基本不等式求得最大值,进而得到所求f(x)的最大值.
解答 解:(Ⅰ)由$p(x)=\left\{\begin{array}{l}108-\frac{1}{3}{x^2},0<x≤10\\ \frac{1080}{x}-\frac{10000}{{3{x^2}}},x>10\end{array}\right.$,
则f(x)=x[p(x)-27]-100=$\left\{\begin{array}{l}81x-\frac{1}{3}{x^3}-100,0<x≤10\\ 980-27x-\frac{10000}{3x},x>10\end{array}\right.$;
(Ⅱ)当0<x≤10时,f'(x)=81-x2,
令f′(x)=0得x=9∈(0,10](x=-9舍去),
且当x∈(0,9)时,f′(x)>0;当x∈(9,10)时,f′(x)<0.
所以当x=9时,f(x)max=f(9)=386.
当x>10时,$f(x)=980-27x-\frac{10000}{3x}$=$980-27(x+\frac{10000}{81x})$
$≤980-27•2\sqrt{x•\frac{10000}{81x}}$=380,
当且仅当$x=\frac{10000}{81x}$即$x=\frac{100}{9}$∈(10,+∞)时取等号.
所以当x>10时,f(x)max=380.
因为386>380,所以当x=9时,f(x)max=386.
答:年产量为9千件时,该工厂在这种产品的生产中所获得的年利润最大.
点评 本题考查函数模型和数学思想的运用,考查分段函数的解析式和最值的求法,注意运用单调性和基本不等式,考查运算能力,属于中档题.

| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学/分 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理/分 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学/分 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理/分 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 17 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
| A. |  圆形区域 | |
| B. |  等腰三角形两腰与半椭圆围成的区域 | |
| C. | 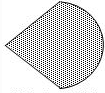 等腰三角形两腰与半圆围成的区域 | |
| D. | 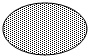 椭圆形区域 |
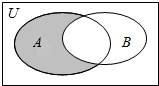 设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )| A. | {1,2,5,6} | B. | {1} | C. | {2} | D. | {1,2,3,4} |
| A. | $[-\frac{5}{4},+∞)$ | B. | [1,2] | C. | $[-\frac{5}{4},1]$ | D. | [-1,1] |
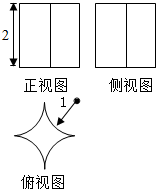 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.