题目内容
已知数列{an}中,a1=2,an+1=3an+2.
(Ⅰ)记bn=an+1,求证:数列{bn}为等比数列;
(Ⅱ)求数列{nan}的前n项和Sn.
(Ⅰ)证明:由an+1=3an+2,可知an+1+1=3(an+1).
∵bn=an+1,∴bn+1=3bn,
又b1=a1+1=3,
∴数列{bn}是以3为首项,以3为公比的等比数列.
(Ⅱ)由(Ⅰ)知 ,得
,得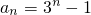 ,∴
,∴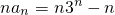 .
.
∴Sn=(1×31+2×32+…+n•3n)-(1+2+…+n)
其中1+2+…+n= =
= ,
,
记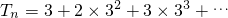 +(n-1)×3n-1+n×3n ①
+(n-1)×3n-1+n×3n ①
∴3Tn=32+2×33+…+(n-1)×3n+n×3n+1 ②
两式相减得-2Tn=3+32+…+3n-n×3n+1=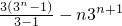 ,
,
∴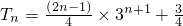 .
.
∴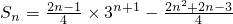 .
.
分析:(I)由an+1=3an+2,可知an+1+1=3(an+1).可得数列{bn}是以a1+1=3为首项,以3为公比的等比数列.
(II)由(I)可得:得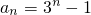 ,于是
,于是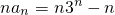 .从而Sn=(1×31+2×32+…+n•3n)-(1+2+…+n),对于前一个括号用“错位相减法”即可求出,后一个括号利用等差数列的前n项和公式即可得出.
.从而Sn=(1×31+2×32+…+n•3n)-(1+2+…+n),对于前一个括号用“错位相减法”即可求出,后一个括号利用等差数列的前n项和公式即可得出.
点评:熟练掌握变形转化为等比数列、“错位相减法”、等差数列的前n项和公式事件他的关键.
∵bn=an+1,∴bn+1=3bn,
又b1=a1+1=3,
∴数列{bn}是以3为首项,以3为公比的等比数列.
(Ⅱ)由(Ⅰ)知
 ,得
,得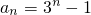 ,∴
,∴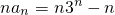 .
.∴Sn=(1×31+2×32+…+n•3n)-(1+2+…+n)
其中1+2+…+n=
 =
= ,
,记
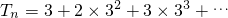 +(n-1)×3n-1+n×3n ①
+(n-1)×3n-1+n×3n ①∴3Tn=32+2×33+…+(n-1)×3n+n×3n+1 ②
两式相减得-2Tn=3+32+…+3n-n×3n+1=
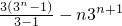 ,
,∴
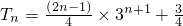 .
.∴
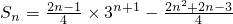 .
.分析:(I)由an+1=3an+2,可知an+1+1=3(an+1).可得数列{bn}是以a1+1=3为首项,以3为公比的等比数列.
(II)由(I)可得:得
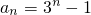 ,于是
,于是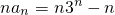 .从而Sn=(1×31+2×32+…+n•3n)-(1+2+…+n),对于前一个括号用“错位相减法”即可求出,后一个括号利用等差数列的前n项和公式即可得出.
.从而Sn=(1×31+2×32+…+n•3n)-(1+2+…+n),对于前一个括号用“错位相减法”即可求出,后一个括号利用等差数列的前n项和公式即可得出.点评:熟练掌握变形转化为等比数列、“错位相减法”、等差数列的前n项和公式事件他的关键.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|