题目内容
18.求出下列两个函数的定义域、奇偶性,并画出图象.(1)y=$\root{3}{{x}^{5}}$,x∈R.
(2)y=$\root{3}{{x}^{4}}$,x∈R.
分析 利用奇偶函数的定义,即可进行判断.
解答 解:(1)x∈R,f(-x)=$\root{3}{(-x)^{5}}$=-$\root{3}{{x}^{5}}$=-f(x),函数是奇函数;
图象如图所示: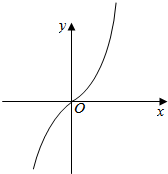
(2)x∈R,g(-x)=$\root{3}{(-x)^{4}}$=$\root{3}{{x}^{4}}$=g(x),函数是偶函数.
图象如图所示: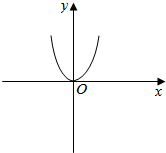
点评 本题考查函数的奇偶性,考查学生的作图能力,比较基础.

练习册系列答案
相关题目
10.下列各组函数,不能表示同一函数的是( )
| A. | f(x)=sin2x,g(x)=2sinxcosx | B. | f(x)=cos2x,g(x)=cos2x-sin2x | ||
| C. | f(x)=2cos2x-1,g(x)=1-2sin2x | D. | f(x)=tan2x,g(x)=$\frac{2tanx}{1-ta{n}^{2}x}$ |