题目内容
已知函数![]() .
.
(1)当x∈[2,4]时.求该函数的值域;
(2)若f(x)≥mlog2x对于x∈[4,16]恒成立,求m的取值范围.
考点:
函数恒成立问题;二次函数在闭区间上的最值.
专题:
函数的性质及应用.
分析:
(1)令t=log4x,则可将函数在x∈[2,4]时的值域问题转化为二次函数在定区间上的值域问题,利用二次函数的图象分析出函数的最值,即可得到函数的值域;
(2)令t=log4x,则可将已知问题转化为2t2﹣3t+1≥2mt对t∈[1,2]恒成立,即![]() 对t∈[1,2]恒成立,求出不等号右边式子的最小值即可得到答案.
对t∈[1,2]恒成立,求出不等号右边式子的最小值即可得到答案.
解答:
解:(1)![]() ,
,
![]()
此时,![]() ,
,
当t=![]() 时,y取最小值
时,y取最小值![]() ,
,
当t=![]() 或1时,y取最大值0,
或1时,y取最大值0,
∴![]()
(2)若f(x)≥mlog2x对于x∈[4,16]恒成立,
令t=log4x,
即2t2﹣3t+1≥2mt对t∈[1,2]恒成立,
∴![]() 对t∈[1,2]恒成立
对t∈[1,2]恒成立
易知![]() 在t∈[1,2]上单调递增
在t∈[1,2]上单调递增
∴g(t)min=g(1)=0,
∴m≤0.
点评:
本题考查的知识点是对数函数的性质,二次函数在闭区间上的最值问题,函数恒成立问题,函数的最值,是函数图象和性质的简单综合应用,难度中档

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,
,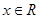 .
.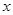 为何值时,
为何值时,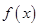 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,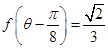 ,求
,求 的值.
的值.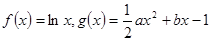 ,
, 且
且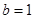 时,证明:对
时,证明:对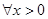 ,
,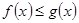 ;
;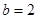 ,且
,且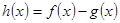 存在单调递减区间,求
存在单调递减区间,求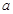 的取值范围;
的取值范围;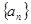 ,若存在常数
,若存在常数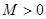 ,
,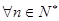 ,都有
,都有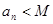 ,则称数列
,则称数列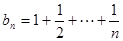 ,试判断数列
,试判断数列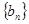 是否有上界.
是否有上界.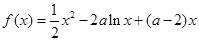 ,
,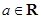 .
.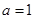 时,求函数
时,求函数 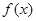 的最小值;
的最小值; 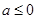 时,讨论函数
时,讨论函数 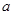 ,对任意的
,对任意的
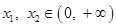 ,且
,且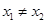 ,有
,有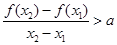 ,恒成立,若存在求出
,恒成立,若存在求出