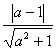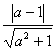题目内容
命题：F1和F2是椭圆的两焦点，P为椭圆上的点，过F2作∠F1PF2的外角平分线的垂线，垂足为T，则T到椭圆中心的距离为该椭圆长轴长的一半．经证明该命题正确．请你依照该命题研究双曲线中的情形，写出类似的正确命题： ．
【答案】分析：根据类比推理的定义，结合椭圆的定义和性质可得得到类比命题．
解答：解：根据椭圆和双曲线性质的和定义，利用椭圆的性质，可以类比是双曲线的命题为：F1和F2为双曲线的两焦点，P 为双曲线上的点，过F2作∠F1PF2的平分线的垂线，垂足为T则T到双曲线中心的距离为该双曲线的实轴长的一半．
故答案：F1和F2为双曲线的两焦点，P 为双曲线上的点，过F2作∠F1PF2的平分线的垂线，垂足为T则T到双曲线中心的距离为该双曲线的实轴长的一半．
点评：本题考查类比推理，考查学生分析解决问题的能力，综合性较强．
解答：解：根据椭圆和双曲线性质的和定义，利用椭圆的性质，可以类比是双曲线的命题为：F1和F2为双曲线的两焦点，P 为双曲线上的点，过F2作∠F1PF2的平分线的垂线，垂足为T则T到双曲线中心的距离为该双曲线的实轴长的一半．
故答案：F1和F2为双曲线的两焦点，P 为双曲线上的点，过F2作∠F1PF2的平分线的垂线，垂足为T则T到双曲线中心的距离为该双曲线的实轴长的一半．
点评：本题考查类比推理，考查学生分析解决问题的能力，综合性较强．
练习册系列答案
相关题目
=1
=1
=1
=1
=1
=1
