题目内容
已知|m|<1,直线l1:y=mx+1,l2:x=-my+1,l1与l2相交于点P,l1交y轴于点A,l2交x轴于点B(1)证明:l1⊥l2;
(2)用m表示四边形OAPB的面积S,并求出S的最大值;
(3)设S=f(m),求U=S+
| 1 | S |
分析:(1)根据斜率之积等于-1,可得故l1⊥l2.
(2)根据四边形OAPB为圆内接四边形,由四边形OAPB的面积S等于两个直角三角形OAB和APB的面积之和,
三角形OAB的面积易求,把l1与l2相的方程联立方程组可解得点P坐标,再求出点P到 AB 的距离,APB的面积
可求.
(3)由函数的导数大于0,可得此函数在定义域内是增函数.
(2)根据四边形OAPB为圆内接四边形,由四边形OAPB的面积S等于两个直角三角形OAB和APB的面积之和,
三角形OAB的面积易求,把l1与l2相的方程联立方程组可解得点P坐标,再求出点P到 AB 的距离,APB的面积
可求.
(3)由函数的导数大于0,可得此函数在定义域内是增函数.
解答:解:(1)由题意知,m≠0,l1与l2的斜率分别为 m,
,斜率之积等于-1,故l1⊥l2.
(2)由题意知,A(0,1),B(1,0),AB=
,四边形OAPB为圆内接四边形(有一组对角互补且都是直角),
把l1与l2相的方程联立方程组可解得点P(
,
),AB 的方程为x+y-1=0,
点P到 AB 的距离为
=
,
由四边形OAPB的面积S等于两个直角三角形OAB和APB的面积之和,
∴S=
×1×1+
×
×
=
+
=
,
故 m=0 时,S有最大值为 1.
(3)U=S+
=
+(1+m2),|m|<1,U的导数U′=
+2m=2m(1-
)>0,
∴U 在其定义域(-1,1)内是单调增函数.
| 1 |
| -m |
(2)由题意知,A(0,1),B(1,0),AB=
| 2 |
把l1与l2相的方程联立方程组可解得点P(
| 1-m |
| 1+m2 |
| 1+m |
| 1+m2 |
点P到 AB 的距离为
|
| ||||
|
| 1-m2 | ||
|
由四边形OAPB的面积S等于两个直角三角形OAB和APB的面积之和,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1-m2 | ||
|
| 1 |
| 2 |
| 1-m2 |
| 2(1+m2) |
| 1 |
| 1+m2 |
故 m=0 时,S有最大值为 1.
(3)U=S+
| 1 |
| S |
| 1 |
| 1+m2 |
| -2m |
| 1+m2 |
| 1 |
| 1+m2 |
∴U 在其定义域(-1,1)内是单调增函数.
点评:本题考查两直线垂直的条件,用分割法求四边形的面积,利用导数判断函数的单调性.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 已知m>1,直线
已知m>1,直线 =0,椭圆C:
=0,椭圆C: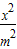 +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点.