Question

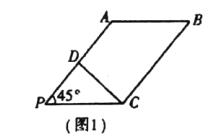
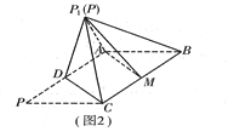
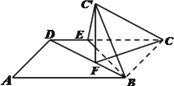
【题目】已知某几何体直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形.

（1）求证： ；

（2）；

（3）设为中点，在边上找一点，使//平面并求.

Answer 1

【答案】（1）见解析（2）（3）

【解析】试题分析：（1）因为该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形, 两两垂直,以为坐标原点,分别以所在直线别为轴建立空间直角坐标系,证出后即可证明平面；〔2〕求出平面的一个法向量,利用与此法向量的夹角的余弦可求出直线与平面所成的角正弦值；（3）设为上一点，由平面，得知，利用向量数量积为求出的值，并求出的值.

试题解析：（1）证明：因为该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，

∴ BA，BC，BB1两两垂直。

以BA，BC，BB1分别为轴建立空间直角坐标系，则N（4,4,0），B1（0, 8,0），C1（0,8,4），C（0,0,4）∵=（4,4,0）·（-4,4,0）=-16+16=0=（4,4,0）·（0,0,4）=0 ∴BN⊥NB1，BN⊥B1C1且NB1与B1C1相交于B1，

∴BN⊥平面C1B1N；

（2）设为平面的一个法向量，则

则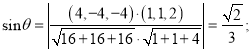

（3）∵M（2,0,0）.设P(0,0,a)为BC上一点,则,

∵MP//平面CNB1,

∴

又,

∴当PB=1时MP//平面CNB1 .

【方法点晴】本题主要考查利用空间向量求二面角、证明线面垂直，求线面角，属于难题. 空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.