Question

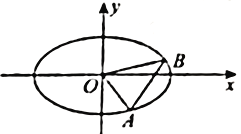
【题目】如图，在矩形中，点在线段上， ， ，沿直线将翻折成，使点在平面上的射影落在直线上.

（Ⅰ）求证：直线平面；

（Ⅱ）求二面角的平面角的余弦值.

Answer 1

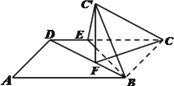
【答案】(1)见解析(2)

【解析】试题分析：（1）根据射影定义得,再根据线面垂直得,最后根据线面垂直判定定理得结论（2）连接交于点.则根据二面角定义得是二面角的平面角的平面角.再通过解三角形得二面角的平面角的余弦值.

试题解析：（Ⅰ）证明：在线段上取点，使，连接交于点.

正方形中， ， 翻折后， ， ，

又 ， 平面，

又 平面， 平面平面

又平面平面 ，

点在平面上的射影落在直线上，

又点在平面上的射影落在直线上，

点为直线与的交点，

平面即平面， 直线平面；

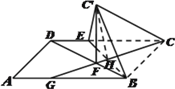
（Ⅱ）由（Ⅰ）得是二面角的平面角的平面角.

，在矩形中，可求得， .

在中， ，

二面角的平面角的余弦值为.

点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.线面角的寻找，主要找射影，即需从线面垂直出发确定射影，进而确定线面角.