题目内容
设等差数列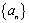 的首项为1,公差d(
的首项为1,公差d(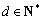 ),m为数列
),m为数列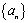 中的项.
中的项.
(1)若d=3,试判断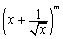 的展开式中是否含有常数项?并说明理由;
的展开式中是否含有常数项?并说明理由;
(2)证明:存在无穷多个d,使得对每一个m,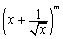 的展开式中均不含常数项.
的展开式中均不含常数项.
(1)解:因为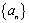 是首项为1,公差为3的等差数列,所以
是首项为1,公差为3的等差数列,所以 .
.
假设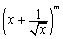 的展开式中的第r+1项为常数项(
的展开式中的第r+1项为常数项( ),
),
 ,于是
,于是 .
.
设
 ,则有
,则有 ,即
,即 ,这与
,这与 矛盾.
矛盾.
所以假设不成立,即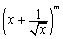 的展开式中不含常数项.
的展开式中不含常数项.
(2)证明:由题设知an= ,设m=
,设m= ,
,
由(1)知,要使对于一切m,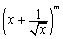 的展开式中均不含常数项,
的展开式中均不含常数项,
必须有:对于 ,满足
,满足 =0的r无自然数解,
=0的r无自然数解,
即
 .
.
当d=3k 时,
时, .
.
故存在无穷多个d,满足对每一个m,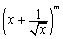 的展开式中均不含常数项.
的展开式中均不含常数项.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 .
. 时,试判断函数
时,试判断函数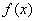 的单调性;
的单调性;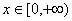 ,
,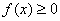 恒成立,求
恒成立,求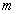 的取值范围;
的取值范围;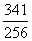 成立的n的取值集合.
成立的n的取值集合.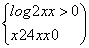 则此函数的“友好点对”有________对.
则此函数的“友好点对”有________对.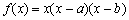 ,点
,点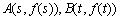 .
.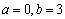 ,函数
,函数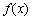 在
在 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求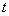 的取值范围;
的取值范围;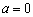 时,
时,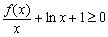 对任意的
对任意的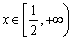 恒成立,求
恒成立,求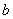 的取值范围;
的取值范围;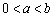 ,函数
,函数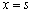 和
和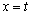 处取得极值,且
处取得极值,且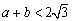 ,
, 是坐标原点,
是坐标原点,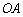 与直线
与直线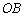 不可能垂直.
不可能垂直. 的最小值是( )
的最小值是( ) C.
C. D.
D.
 则z=
则z= 的取值范围是( )
的取值范围是( ) B.
B. C.
C.  D.
D.
 的值为( )
的值为( ) ,则
,则  ( )
( ) B
B  D
D 