题目内容
11.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则$\frac{{{a^2}+{e^2}}}{2b}$的最小值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 由题意画出图形,利用转化思想方法求得OQ=a,又OQ=2b,得a=2b,进一步得到a,e与b的关系,然后利用基本不等式求得$\frac{{{a^2}+{e^2}}}{2b}$的最小值.
解答  解:如图,由题意,P是以F1,F2为焦点的椭圆上一点,
解:如图,由题意,P是以F1,F2为焦点的椭圆上一点,
过焦点F2作∠F1PF2外角平分线的垂线,垂足为Q,
延长F2Q交F1P延长线于M,得PM=PF2,
由椭圆的定义知PF1+PF2=2a,故有PF1+PM=MF1=2a,
连接OQ,知OQ是三角形F1F2M的中位线,
∴OQ=a,又OQ=2b,
∴a=2b,则a2=4b2=4(a2-c2),
即c2=$\frac{3}{4}$a2,
∴$\frac{{a}^{2}+{e}^{2}}{2b}$=$\frac{{a}^{4}+{c}^{2}}{2{a}^{2}b}$=$\frac{16{b}^{4}+\frac{3}{4}•4{b}^{2}}{8{b}^{3}}$
=2b+$\frac{3}{8b}$≥2$\sqrt{2b•\frac{3}{8b}}$=$\sqrt{3}$.
当且仅当2b=$\frac{3}{8b}$,即b=$\frac{\sqrt{3}}{4}$时,$\frac{{a}^{2}+{e}^{2}}{2b}$有最小值为$\sqrt{3}$.
故选:C.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.对任意非零实数a,b,若a?b的运算原理如图所示,则20.5?log0.5$\frac{1}{4}$的值为( )
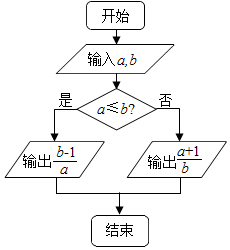

| A. | $\frac{{\sqrt{2}+1}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}-1}}{2}$ |
16.执行如图所示的程序框图,如果输入的t=50,则输出的n=( )
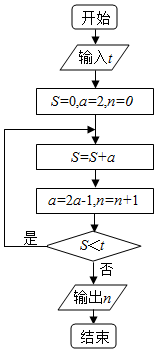

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
3.执行如图所示的程序框图,则该程序运行后输出的i值为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |