Question

【题目】如图所示，直四棱柱的侧棱长为，底面是边长的矩形，为的中点，

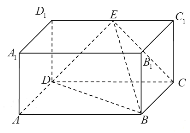
（1）求证：平面，

（2）求异面直线与所成的角的大小（结果用反三角函数表示）.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）先证明EC⊥ED，再利用BC⊥平面CC1D1D，证明BC⊥DE，即可证明DE⊥平面EBC；

（2）取A1B1中点F，连接BF,DF,∠FBD即为所求异面直线的夹角（或其补角），确定△FBD为各边长，根据余弦定理可求∠FBD余弦值，从而求异面直线BD与EC所成的角的大小．

(1)证明：∵直四棱柱的侧棱长为,

底面ABCD是边长AB=2a,BC=a的矩形,

为的中点，

∴EC=ED=a，CD=2a，

∴EC⊥ED,

∵BC⊥平面,DE平面，

∴BC⊥DE,

∵BC∩EC=C

∴DE⊥平面EBC.

(2)取A1B1中点F，连接BF,DF,

易得EC∥FB，

∴∠FBD即为所求异面直线的夹角(或其补角),

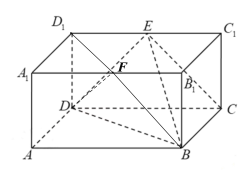
连接D1F，△DD1F为直角三角形，

∴，

∴，

又，

根据余弦定理,，

∴，

∴异面直线与所成的角的大小为.