题目内容
求下列双曲线的标准方程:(1)与椭圆![]() =1共焦点,且过点(-2,
=1共焦点,且过点(-2,![]() )的双曲线.
)的双曲线.
(2)与椭圆![]() =1有共同焦点,且在y轴右侧与此椭圆的一个交点的纵坐标为4的双曲线.
=1有共同焦点,且在y轴右侧与此椭圆的一个交点的纵坐标为4的双曲线.
解:(1)由![]() =1知F1(0,-3),F2(0,3).
=1知F1(0,-3),F2(0,3).
设双曲线的方程为![]() =1(a>0,b>0),则有
=1(a>0,b>0),则有 ∴a2=5,b2=4.
∴a2=5,b2=4.
∴所求的双曲线的方程为![]() =1.
=1.
(2)由已知得双曲线两焦点分别为F1(0,-3),F2(0,3),
设双曲线的方程为![]() =1(a>0,b>0),
=1(a>0,b>0),
∵在y轴右侧双曲线与椭圆有一交点纵坐标为4,
∴它们交点为A(![]() ,4).
,4).
∵||AF1|-|AF2||=2a,∴将A、F1、F2的坐标代入得a=2.
又∵c=3,∴b2=c2-a2=5,
故所求双曲线的方程为![]() =1.
=1.

练习册系列答案
相关题目
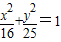 共焦点,且过点
共焦点,且过点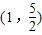 的双曲线;
的双曲线;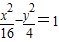 有相同渐近线,且过点
有相同渐近线,且过点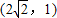 的双曲线.
的双曲线.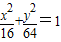 有相同的焦点,且离心率为
有相同的焦点,且离心率为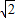 .
.