题目内容
求下列双曲线的标准方程.
(1)与椭圆
+
=1共焦点,且过点(1,
)的双曲线;
(2)与双曲线
-
=1有相同渐近线,且过点(2
,1)的双曲线.
(1)与椭圆
| x2 |
| 16 |
| y2 |
| 25 |
| 5 |
| 2 |
(2)与双曲线
| x2 |
| 16 |
| y2 |
| 4 |
| 2 |
(1)椭圆
+
=1焦点坐标为(0,3),在y轴上
∴所求双曲线的焦点坐标为(0,3),c=3
故设双曲线方程为
-
=1
∵点(1,
)在双曲线上
∴
-
=1解得a2=5,
∴所求双曲线方程为
-
=1
(2)与双曲线
-
=1有相同渐近线的双曲线方程可设为
-
=λ
而点(2
,1)在双曲线上则
-
=λ解得λ=
∴所求双曲线方程为
-y2=1
| x2 |
| 16 |
| y2 |
| 25 |
∴所求双曲线的焦点坐标为(0,3),c=3
故设双曲线方程为
| y2 |
| a2 |
| x2 |
| 9-a2 |
∵点(1,
| 5 |
| 2 |
∴
(
| ||
| a2 |
| 12 |
| 9-a2 |
∴所求双曲线方程为
| y2 |
| 5 |
| x2 |
| 4 |
(2)与双曲线
| x2 |
| 16 |
| y2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
而点(2
| 2 |
(2
| ||
| 16 |
| 12 |
| 4 |
| 1 |
| 4 |
∴所求双曲线方程为
| x2 |
| 4 |

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
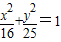 共焦点,且过点
共焦点,且过点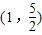 的双曲线;
的双曲线;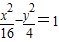 有相同渐近线,且过点
有相同渐近线,且过点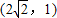 的双曲线.
的双曲线.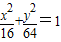 有相同的焦点,且离心率为
有相同的焦点,且离心率为 .
.