题目内容
已知曲线C1的极坐标方程为ρcos(θ- )=-1,曲线C2的极坐标方程为ρ=2
)=-1,曲线C2的极坐标方程为ρ=2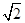 cos(θ-
cos(θ- ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
(Ⅰ) ; (Ⅱ)
; (Ⅱ) .
.
解析试题分析:(Ⅰ)先化简 ,再利用
,再利用 ,
, 代入即可得
代入即可得 ;(Ⅱ)先化简得
;(Ⅱ)先化简得 的直角坐标方程为
的直角坐标方程为 ,再求
,再求 的圆心
的圆心 到直线的距离
到直线的距离 ,所以动点
,所以动点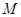 到曲线
到曲线 的距离的最大值为
的距离的最大值为 .
.
试题解析:(Ⅰ) ,
,
即 ,可得
,可得 ,
,
故 的直角坐标方程为
的直角坐标方程为 . (5分)
. (5分)
(Ⅱ) 的直角坐标方程为
的直角坐标方程为 ,
,
由(Ⅰ)知曲线 是以
是以 为圆心的圆,且圆心到直线
为圆心的圆,且圆心到直线 的距离
的距离 ,
,
所以动点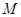 到曲线
到曲线 的距离的最大值为
的距离的最大值为 . (10分)
. (10分)
考点:1.极坐标方程;2.点到直线的距离公式.

练习册系列答案
相关题目
极坐标方程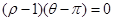
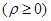 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.两条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
圆 的圆心坐标是( )
的圆心坐标是( )
A. | B. | C. | D. |
在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 |
B.θ=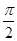 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=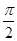 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 |
| D.θ=0(ρ∈R)和ρcos θ=1 |
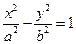 (a>1,b>0)的焦距为2c,直线
(a>1,b>0)的焦距为2c,直线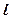 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线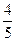 c.求双曲线的离心率e的取值范围.
c.求双曲线的离心率e的取值范围. 轴的非负半轴为极轴建立极坐标系,则线段
轴的非负半轴为极轴建立极坐标系,则线段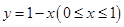 的极坐标为( )
的极坐标为( )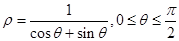
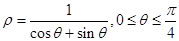


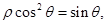 曲线C2的参数方程为
曲线C2的参数方程为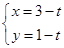 (
(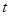 为参数),以极点为原点,极轴为
为参数),以极点为原点,极轴为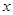 轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为
轴正半轴建立平面直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为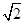
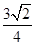
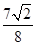
 ,
, ,
, ,
, ,点
,点 分别在线段
分别在线段
 上运动,且
上运动,且 ,设
,设 与
与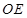 交于点
交于点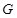 ,则点
,则点



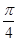 的直线
的直线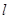 与曲线
与曲线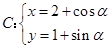 ,(
,(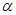 为参数)交于
为参数)交于 、
、 两点,且
两点,且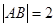 ,以坐标原点
,以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则直线
轴正半轴为极轴建立极坐标系,则直线