题目内容
已知a,b∈R,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:若 ,又
,又 ,所以
,所以
 ;反之则不一定成立,比如
;反之则不一定成立,比如 ,但
,但 .所以是充分条件,但不是必要条件.选A.
.所以是充分条件,但不是必要条件.选A.
考点:1、充要条件;2、不等关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
下列命题中的假命题是( )
A. | B. |
C. | D. |
已知命题 :“
:“ ,
, ”,那么
”,那么 是( )
是( )
A. , , , , | B. , , |
C. , , | D. , , |
已知函数 则
则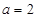 是
是 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p: ,且a>0,有
,且a>0,有 ,命题q:
,命题q: ,
, ,则下列判断正确的是
,则下列判断正确的是
| A.p是假命题 | B.q是真命题 |
C. 是真命题 是真命题 | D. 是真命题 是真命题 |
设 为向量。则
为向量。则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也必要条件 |
下列命题的否定为假命题的是( )
A. | B. , , |
| C.所有能被3整除的整数都是奇数 | D. |
“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分不必要条件; | B.必要不充分条件; |
| C.充要条件; | D.既不充分也不必要条件; |
已知命题p:“?x∈[0,1],a≥ex”,命题q:“?x∈R,x2+4x+a=0”,若命题“p∧q”是真命题;则实数a的取值范围是( )
| A.(4,+∞) | B.[1,4] | C.[e,4] | D.(-∞,1] |