Question

【题目】已知f（x）=ex与g（x）=ax+b的图象交于P（x1 ， y1），Q（x2 ， y2）两点． （Ⅰ）求函数h（x）=f（x）﹣g（x）的最小值；
（Ⅱ）且PQ的中点为M（x0 ， y0），求证：f（x0）＜a＜y0 ．

Answer 1

【答案】解：（Ⅰ）h（x）=ex﹣ax﹣b，求导得h'（x）=ex﹣a 当a≤0时，h'（x）＞0，h（x）在R上为增函数，不满足有两个零点，故不合题意；
所以a＞0，令h'（x）=0，解得x=lna，
并且有x∈（﹣∞，lna），h'（x）＜0；x∈（lna，+∞），h'（x）＞0，
故 ．
（Ⅱ）证明：要证f（x0）＜a＜y0成立，
即证 ，不妨设x2＞x1 ，
只需证 ，
即为 ，
要证 ，只需证 ，
令 ，
只需证F（t）＞0，求导 ，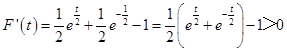
∴F（t）在（0，+∞）为增函数，
故F（t）＞F（0）=0，
∴ ；
要证 ，
只需证明 ，
令 ，
求导 ，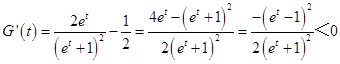
∴G（t）在（0，+∞）为减函数，故G（t）＜G（0）=0，
∴ ；
∴ ，t＞0，成立，
∴f（x0）＜a＜y0成立
【解析】（Ⅰ）先求导，利用导数求出函数最小值即可， （Ⅱ）利用分析法，要证f（x0）＜a＜y0 ， 只需证 ，构造函数 ，利用导数只需证明 ，再构造函数，根据导数和函数的单调性的关系即可证明
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案，需要熟知利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．