题目内容
如图求证:G、E、A、F四点共圆.
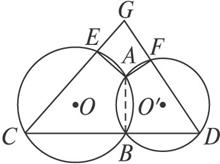
图
证明:连结AB,
∵四边形AECB内接于⊙O,
∴∠GEA=∠ABC.
∵四边形ABDF内接于⊙O′,
∴∠GFA=∠ABD.
∵∠ABC+∠ABD=180°,
∴∠GEA+∠GFA=180°.
∴G、E、A、F四点共圆.
练习册系列答案
相关题目
题目内容
如图求证:G、E、A、F四点共圆.
图
证明:连结AB,
∵四边形AECB内接于⊙O,
∴∠GEA=∠ABC.
∵四边形ABDF内接于⊙O′,
∴∠GFA=∠ABD.
∵∠ABC+∠ABD=180°,
∴∠GEA+∠GFA=180°.
∴G、E、A、F四点共圆.
)请你观察并计算需求面积在100～140(含140,不含100)m2的客户数是___________________. 
=m，
=n,
=p,
=q,
=r，求作向量m-p+n-q-r.