题目内容
(1)已知锐角α,β满足 ,
, ,求cos(α-β)的值.
,求cos(α-β)的值.(2)若锐角α,β满足
 ,
, ,求sinβ的值.
,求sinβ的值.
【答案】分析:(1)先利用同角三角函数的基本关系和α、β的范围,求得cosα和sinβ的值,进而利用余弦函数的两角和公式求得答案.
(2)根据cosα和cos(α+β)的值,利用同角三角函数的基本关系求得sinα和sin(α+β)的值,进而根据sinβ=sin[(α+β)-α]利用两角和公式求得答案.
解答:解:(1)∵α、β为锐角,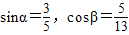
∴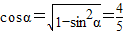
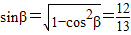
∴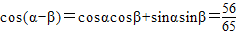
(2)∵α为锐角,且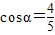 ,
,
∴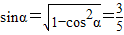
又∵β为锐角,且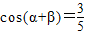 ,
,
∴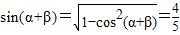
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=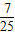
点评:本题主要考查了同角三角函数的基本关系的应用和两角和公式的化简求值.重点考查了三角函数基础知识的运用.
(2)根据cosα和cos(α+β)的值,利用同角三角函数的基本关系求得sinα和sin(α+β)的值,进而根据sinβ=sin[(α+β)-α]利用两角和公式求得答案.
解答:解:(1)∵α、β为锐角,
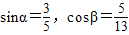
∴
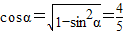
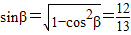
∴
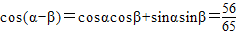
(2)∵α为锐角,且
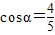 ,
,∴
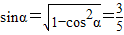
又∵β为锐角,且
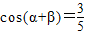 ,
,∴
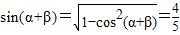
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=
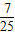
点评:本题主要考查了同角三角函数的基本关系的应用和两角和公式的化简求值.重点考查了三角函数基础知识的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,求cos(α-β)的值.
,求cos(α-β)的值. ,
, ,求sinβ的值.
,求sinβ的值. 满足
满足 ,
, ,求
,求 的值;
的值; 满足
满足 ,
, ,求
,求 的值。
的值。