题目内容
已知在△ABC中，（a+b）：（b+c）：（c+a）=4：6：5，则sinA：sinB：sinC= ．
考点：正弦定理
专题：解三角形
分析：由（a+b）：（b+c）：（c+a）=4：6：5，解得a：b：c=3：5：7，再利用正弦定理即可得出．
解答：
解：∵a+b）：（b+c）：（c+a）=4：6：5，
∴
=
=
=k＞0．
解得a：b：c=3：5：7，
则sinA：sinB：sinC=3：5：7．
故答案为：3：5：7．
∴
| a+b |
| 4 |
| b+c |
| 6 |
| c+a |
| 5 |
解得a：b：c=3：5：7，
则sinA：sinB：sinC=3：5：7．
故答案为：3：5：7．
点评：本题考查了正弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设非负实数x，y满足
，则z=3x+2y的最大值是（ ）
|
| A、7 | B、6 | C、9 | D、12 |
执行如图的程序，若输入的x=2，则输出的所有x的值的和为（ ）
| A、6 | B、21 | C、101 | D、126 |
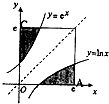如图，在边长为e（e为自然对数的底数）的正方形区域的A处于C处各有一个通信基站，其信号覆盖范围分别为如图所示的阴影区域．该正方形区域内无其它信号来源且这两个基站工作正常，若在该正方形区域内随机选择一个地点，则该地点无信号的概率为（ ）
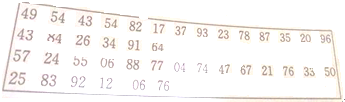福利彩票“双色球”中，红球号码有编号为01，02，…，33的33个个体组成，某彩民利用下面的随机数表选取6组数作为6个红球的编号，选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字，则选出来的第6个红球的编号为（ ）