题目内容
正态总体N(0,1)的概率密度函数是f(x)=(1)求证:f(x)是偶函数;
(2)求f(x)的最大值;
(3)利用指数函数的性质说明f(x)的增减性.
思路分析: 对给出的标准正态分布的概率密度函数,可以利用函数的相关知识来研究它的相关性质.
解:(1)对于任意的x∈R,f(-x)=![]() =
=![]() =f(x).
=f(x).
所以f(x)是偶函数;
(2)令z=![]() ,当x=0时,z=0,ex=1,
,当x=0时,z=0,ex=1,
∵ex是关于z的增函数,当x≠0时,z>0,ex>1,
∴当x=0,即z=0时,![]() =ex取得最小值,当x=0时,f(x)=
=ex取得最小值,当x=0时,f(x)=![]() 取得最大值
取得最大值![]()
(3)任取x1<0,x2<0,且x1<x2,有x12>x22,
∴![]()
所以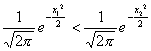 ,即f(x1)<f(x2).
,即f(x1)<f(x2).
这表明当x<0时,f(x)是递增的.同理可得,对于任取的x1>0,x2>0,且x1<x2,有f(x1)>f(x2),即当x>0时,f(x)是递减的.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目