Question

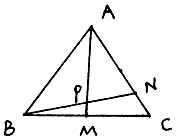
【题目】如图所示，在△ABC中，点M是BC的中点，点N在AC上，且AN=3NC，AM与BN相交于点P，设 = ， = ，用 、 表示 ．

Answer 1

【答案】解：设 =λ = λ（ + ）= （ + ）= + ， ∵B，P，N三点共线，
∴ + =1，
∴λ=
∴ = + = + = + （ + ）
= + （ ﹣ ）+ = + = +
【解析】设 =λ ，根据B，P，N三点共线，求出λ= ，再根据根据向量加法的几何意义，向量的数乘运算，即可求出
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使才能正确解答此题．