Question

已知等腰△ABC中，AC=BC，且A(2，1)，B(-4，3)，求点C的轨迹．

Answer 1

思路分析：根据题意，先设点C(x，y)，又由CA=CB，∴借助两点间距离公式即可得C点轨迹方程，这是“直接法”．但此例中，由题意能够断定点C的轨迹是一条直线，具体地说就是线段AB的中垂线，而确定直线方程，可利用待定系数法．

解：如图，设AB的中点D,

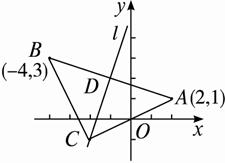
∵A(2，1)，B(-4，3)，

∴D(-1，2).

∴过点D的直线l：y-2=k(x+1).

∵直线l⊥AB,

∴k·k_AB=-1，而k_AB=，∴k=3.

    则l：y-2=3(x+1),即：3x-y+5=0.

    但点C不能与点D重合，否则不能构成三角形．

    故点C的轨迹为直线：3x-y+5=0，除去(-1，2)点．

方法归纳 在求轨迹方程时，若不注意检验，往往会产生丢解或多解情况，而“数形结合”有时会帮助我们解决这个问题．