题目内容
已知Rt△ABC两锐角A,B的正弦值,是实系数方程2x2-2
kx+5k-3=0的两根.若数列{an}满足an+1=2an-
k(n∈N*),且a1=5.试求数列{an}的前n项和为Tn.
| 3 |
| 3 |
| 2 |
分析:由题意可得x1=sinA,x2=sinB=sin(
-A)=cosA,结合同角平分关系sin2A+cos2A=1可得x12+x22=1,由方程的根与系数关系可求k=1或k=
,经检验当k=1时,无解不合题意;当k=
时,符合题意,代入可得an+1=2an-
k(n∈N*),从而可得 {an-1}是等比数列,可求an,由等比数列的求和公式及分组求和的方法可求
| π |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
解答:解:∵方程的两根是一个直角三角形的两锐角A、B的正弦,
令x1=sinA,x2=sinB=cosA
∵sin2A+cos2A=1
∴x12+x22=1
∵x1+x2=
k,x1x2=
∴3k2-2×
=1,
即3k2-5k+2=0
∴k=1或k=
.
当k=1时,原方程为x2-
x+1=0,△<0,不合题意.
当k=
时,原方程为2x2-
x+
=0,x1,x2∈(0,1),符合题意.
∵an+1=2an-
k(n∈N*),
∴an+1=2an-1(n∈N*),an+1-1=2(an-1)(n∈N*),
从而 {an-1}是等比数列,an=2n+1+1
∴Tn=22+23+…+2n+1+n=
+n=2n+2+n-4.
令x1=sinA,x2=sinB=cosA
∵sin2A+cos2A=1
∴x12+x22=1
∵x1+x2=
| 3 |
| 5k-3 |
| 3 |
∴3k2-2×
| 5k-3 |
| 2 |
即3k2-5k+2=0
∴k=1或k=
| 2 |
| 3 |
当k=1时,原方程为x2-
| 3 |
当k=
| 2 |
| 3 |
4
| ||
| 3 |
| 1 |
| 3 |
∵an+1=2an-
| 3 |
| 2 |
∴an+1=2an-1(n∈N*),an+1-1=2(an-1)(n∈N*),
从而 {an-1}是等比数列,an=2n+1+1
∴Tn=22+23+…+2n+1+n=
| 4(1-2n) |
| 1-2 |
点评:本题是一元二次方程与三角函数相结合的题目,由递推公式构造等比数列求数列的通项公式,正确理解一元二次方程的根的判别式以及锐角三角函数的性质是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为
(A)(不等式选做题)不等式|x+1|-|x-2|>2的解集为 (A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
(A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为= 的两根.若数列{an}满足
的两根.若数列{an}满足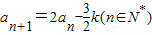 ,且a1=5.试求数列{an}的前n项和为Tn.
,且a1=5.试求数列{an}的前n项和为Tn.