Question

如图,在正方体ABCD—A₁B₁C₁D₁中,M、N分别为棱A₁B₁、A₁D₁的中点,E、F分别为棱B₁C₁、C₁D₁的中点.求证:

(1)E、F、B、D四点共面;

(2)平面AMN∥平面EFDB.

Answer 1

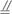
思路分析：由于图中有很多中点,因此可以考虑证线线平行而获得四点共面以及面面平行.

证明:(1)连结D₁B₁、DB,

    ∵B₁BD₁D,

    ∴D₁B₁∥DB.

    而EF∥D₁B₁,∴EF∥DB.

    ∴E、F、B、D共面.

    (2)连结NE,则NEA₁B₁AB,

    ∴NABE是平行四边形.

    ∴AN∥BE.∴AN∥平面EFDB.

    又∵NM∥D₁B₁∥EF,

    ∴NM∥平面EFDB.

    而AN、NM是平面AMN内的两条相交直线,由平面和平面平行的判定定理可知,面AMN∥面EFDB.