题目内容
下列几个命题:①不等式
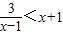 的解集为{x|x<-2,或x>2};
的解集为{x|x<-2,或x>2};②已知a,b均为正数,且
 ,则a+b的最小值为9;
,则a+b的最小值为9;③已知m2+n2=4,x2+y2=9,则mx+ny的最大值为
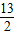 ;
;④已知x,y均为正数,且x+3y-2=0,则3x+27y+1的最小值为7;
其中正确的有 .(以序号作答)
【答案】分析:①不等式 的解集为{x|-2<x<1,或x>2};
的解集为{x|-2<x<1,或x>2};
②由a,b均为正数,且 ,知a+b=(
,知a+b=( )(a+b)=5+
)(a+b)=5+ ≥5+2
≥5+2 =9;
=9;
③由m2+n2=4,x2+y2=9,设 ,
, ,则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),故mx+ny的最大值为6;
,则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),故mx+ny的最大值为6;
④由x,y均为正数,且x+3y-2=0,知3x+27y+1 =7.
=7.
解答:解:不等式 的解集为{x|-2<x<1,或x>2},故①不成立;
的解集为{x|-2<x<1,或x>2},故①不成立;
∵a,b均为正数,且 ,
,
a+b=( )(a+b)=5+
)(a+b)=5+ ≥5+2
≥5+2 =9,故②正确;
=9,故②正确;
∵m2+n2=4,x2+y2=9,
∴设 ,
, ,
,
则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),
∵-1≤cos(α-β)≤1,
∴mx+ny的最大值的最大值为6,故③不正确;
④∵x,y均为正数,且x+3y-2=0,
∴3x+27y+1 =7,故④正确.
=7,故④正确.
故答案为:②④.
点评:本题考查真假命题的判断,解题时要注意不等式、均值定理、三角函数等知识点的灵活运用.
 的解集为{x|-2<x<1,或x>2};
的解集为{x|-2<x<1,或x>2};②由a,b均为正数,且
 ,知a+b=(
,知a+b=( )(a+b)=5+
)(a+b)=5+ ≥5+2
≥5+2 =9;
=9;③由m2+n2=4,x2+y2=9,设
 ,
, ,则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),故mx+ny的最大值为6;
,则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),故mx+ny的最大值为6;④由x,y均为正数,且x+3y-2=0,知3x+27y+1
 =7.
=7.解答:解:不等式
 的解集为{x|-2<x<1,或x>2},故①不成立;
的解集为{x|-2<x<1,或x>2},故①不成立;∵a,b均为正数,且
 ,
,a+b=(
 )(a+b)=5+
)(a+b)=5+ ≥5+2
≥5+2 =9,故②正确;
=9,故②正确;∵m2+n2=4,x2+y2=9,
∴设
 ,
, ,
,则mx+ny=6sinαsinβ+6cosαcosβ=6cos(α-β),
∵-1≤cos(α-β)≤1,
∴mx+ny的最大值的最大值为6,故③不正确;
④∵x,y均为正数,且x+3y-2=0,
∴3x+27y+1
 =7,故④正确.
=7,故④正确.故答案为:②④.
点评:本题考查真假命题的判断,解题时要注意不等式、均值定理、三角函数等知识点的灵活运用.

练习册系列答案
相关题目