题目内容
两个数列{an},{bn},满足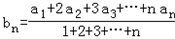 .(参考公式
.(参考公式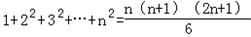 )
)
求证:{bn}为等差数列的充要条件是{an}为等差数列.
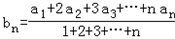 .(参考公式
.(参考公式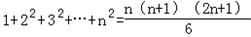 )
)求证:{bn}为等差数列的充要条件是{an}为等差数列.
证明:∵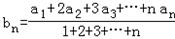 ,
,
∴bn+1=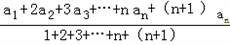 ,
,
∴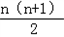 bn=a1+2a2+3a3+…+nan ①,
bn=a1+2a2+3a3+…+nan ①,
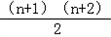 bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
②减去①可得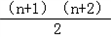 bn+1﹣
bn+1﹣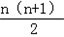 bn=(n+1)an+1.
bn=(n+1)an+1.
两边同时除以n+1可得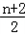 bn+1﹣
bn+1﹣ bn=an+1 ③,
bn=an+1 ③,
∴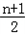 bn﹣
bn﹣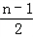 bn﹣1=an ④.
bn﹣1=an ④.
③减去④可得 an+1 ﹣an=(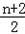 bn+1 ﹣
bn+1 ﹣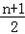 bn )﹣(
bn )﹣( bn ﹣
bn ﹣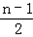 bn﹣1 )
bn﹣1 )
= bn+1 +bn+1 ﹣
bn+1 +bn+1 ﹣ bn﹣
bn﹣ bn﹣
bn﹣ bn+
bn+ bn﹣1﹣
bn﹣1﹣ bn﹣1
bn﹣1
= (bn+1﹣bn )+
(bn+1﹣bn )+ (bn+1﹣bn )+
(bn+1﹣bn )+ (bn﹣bn﹣1)﹣
(bn﹣bn﹣1)﹣ (bn﹣bn﹣1)
(bn﹣bn﹣1)
=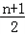 (bn+1﹣bn )+
(bn+1﹣bn )+ (bn+1﹣bn )﹣
(bn+1﹣bn )﹣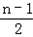 (bn﹣bn﹣1).
(bn﹣bn﹣1).
由于{bn}为等差数列的充要条件是 bn+1﹣bn=bn﹣bn﹣1=常数d,
此时an+1 ﹣an=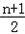 d+
d+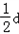 ﹣
﹣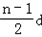 =
=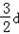 ,是个常数.
,是个常数.
故:{bn}为等差数列的充要条件是{an}为等差数列.
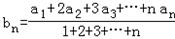 ,
,∴bn+1=
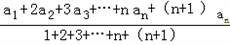 ,
,∴
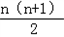 bn=a1+2a2+3a3+…+nan ①,
bn=a1+2a2+3a3+…+nan ①,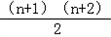 bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②
bn+1=a1+2a2+3a3+…+nan+(n+1)an+1.②②减去①可得
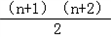 bn+1﹣
bn+1﹣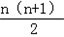 bn=(n+1)an+1.
bn=(n+1)an+1.两边同时除以n+1可得
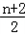 bn+1﹣
bn+1﹣ bn=an+1 ③,
bn=an+1 ③,∴
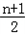 bn﹣
bn﹣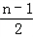 bn﹣1=an ④.
bn﹣1=an ④.③减去④可得 an+1 ﹣an=(
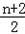 bn+1 ﹣
bn+1 ﹣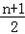 bn )﹣(
bn )﹣( bn ﹣
bn ﹣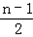 bn﹣1 )
bn﹣1 )=
 bn+1 +bn+1 ﹣
bn+1 +bn+1 ﹣ bn﹣
bn﹣ bn﹣
bn﹣ bn+
bn+ bn﹣1﹣
bn﹣1﹣ bn﹣1
bn﹣1=
 (bn+1﹣bn )+
(bn+1﹣bn )+ (bn+1﹣bn )+
(bn+1﹣bn )+ (bn﹣bn﹣1)﹣
(bn﹣bn﹣1)﹣ (bn﹣bn﹣1)
(bn﹣bn﹣1)=
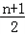 (bn+1﹣bn )+
(bn+1﹣bn )+ (bn+1﹣bn )﹣
(bn+1﹣bn )﹣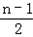 (bn﹣bn﹣1).
(bn﹣bn﹣1).由于{bn}为等差数列的充要条件是 bn+1﹣bn=bn﹣bn﹣1=常数d,
此时an+1 ﹣an=
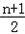 d+
d+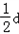 ﹣
﹣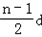 =
=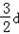 ,是个常数.
,是个常数.故:{bn}为等差数列的充要条件是{an}为等差数列.

练习册系列答案
相关题目