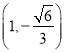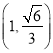题目内容
【题目】设椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其中一个焦点为圆
,其中一个焦点为圆![]() 的圆心,右顶点是圆
的圆心,右顶点是圆![]() 与
与![]() 轴的一个交点.已知椭圆
轴的一个交点.已知椭圆![]() 与直线
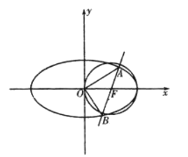
与直线![]() 相交于
相交于![]() 、
、![]() 两点,延长
两点,延长![]() 与椭圆
与椭圆![]() 交于点
交于点![]() .
.
(1)求椭圆的方程;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)3
(2)3
【解析】
(1)求出![]() 圆心,以及与
圆心,以及与![]() 轴的的交点(圆心右侧),为椭圆的右顶点,即可求出椭圆方程;
轴的的交点(圆心右侧),为椭圆的右顶点,即可求出椭圆方程;
(2)根据椭圆的对称性![]() ,设
,设![]() ,直线
,直线![]() 过
过![]() ,
,![]() ,椭圆方程与直线方程联立,消去
,椭圆方程与直线方程联立,消去![]() ,得到关于
,得到关于![]() 的一元二次方程,利用韦达定理,求出
的一元二次方程,利用韦达定理,求出![]() 关于
关于![]() 为变量的函数,运用换元法,结合求导,求出函数的最值,即为
为变量的函数,运用换元法,结合求导,求出函数的最值,即为![]() 面积的最大值.
面积的最大值.
(1)圆![]() ,化为
,化为![]() ,
,
圆心![]() ,与
,与![]() 轴交点坐标
轴交点坐标![]() ,
,
右顶点为![]() ,所求的椭圆方程为
,所求的椭圆方程为![]() .
.
(2)设![]() ,
,![]() ,
,
由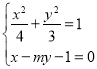 得,
得,![]() .
.
![]() ,
,![]()
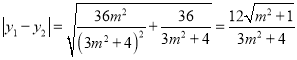
![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
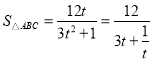 ,
,
设![]() ,
,![]() 恒成立,
恒成立,
![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 取得最小值,
取得最小值,
此时![]() 取得最大值为3.
取得最大值为3.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目