Question

7．已知定圆C₁：x²+y²+4x=0与C₂：x²+y²-4x-60=0，动圆M与圆C₁外切，与圆C₂内切，求动圆圆心的轨迹方程．

Answer 1

分析 化圆的一般方程为标准方程，求出圆心和半径，作出图形，利用动圆M与圆C₁外切，与圆C₂内切，可得|MC₁|+|MC₂|=10＞|C₁C₂|=4．即动圆圆心的轨迹是以C₁，C₂为焦点，长半轴长为5的椭圆，则动圆圆心的轨迹方程可求．

解答 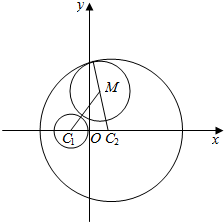解：由C₁：x²+y²+4x=0，得（x+2）²+y²=4，
C₂：x²+y²-4x-60=0，得（x-2）²+y²=64，
∴圆C₁的圆心坐标为（-2，0），半径为2，圆C₂的圆心坐标为（2，0），半径为8．
如图，设动圆M的半径为r，
∵动圆M与圆C₁外切，与圆C₂内切，
∴|MC₁|=r+2，|MC₂|=8-r，
则|MC₁|+|MC₂|=10＞|C₁C₂|=4．
∴动圆圆心的轨迹是以C₁，C₂为焦点，长半轴长为5的椭圆，
∵a=5，c=2，∴b²=a²-c²=21．
∴M的轨迹方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{21}=1$．

点评 本题考查圆与圆的位置关系，考查了椭圆的定义，属中档题．