题目内容
 已知an=2n,把数列{an}的各项排成如图三角形状,记A(i,j)表示第i行中第j个数,则结论
已知an=2n,把数列{an}的各项排成如图三角形状,记A(i,j)表示第i行中第j个数,则结论①A(2,3)=16;
②A(i,3)=2A(i,2)(i≥2);
③[A(i,i)]2=A(i,1)•A(i,2i-1),(i≥1);
④A(i+1,1)=A(i,1)•22i-1,(i≥1);
其中正确的是
分析:观察三角形中第i行最后一个数的下脚标,得知下脚标值是该行的行数的平方,从而得到A(i,j)的表达式,
再依次分析①②③④,可判断其正确性.
再依次分析①②③④,可判断其正确性.
解答:解:依题意知,①A(2,3)=a4=24=16;即①正确;
由图可知,第i行最后一个数是ai2,
∴②A(i,3)=a(i-1)2+3=2i2-2i+4,
A(i,2)=a(i-1)2+2=2i2-2i+3
∴A(i,3)=2A(i,2)(i≥2);即②正确;
③[A(i,i)]2=(a(i-1)2+i)2=(2i2-i+1)2
A(i,1)•A(i,2i-1)=2i2-2i+2•2i2=22(i2-i+1)=(2i2-i+1)2=[A(i,i)]2,即③正确;
④A(i+1,1)=ai2+1=2i2+1,A(i,1)•22i-1=2i2-2i+2•22i-1=2i2+1
∴A(i+1,1)=A(i,1)•22i-1,即④正确;
故答案为:①②③④.
由图可知,第i行最后一个数是ai2,
∴②A(i,3)=a(i-1)2+3=2i2-2i+4,
A(i,2)=a(i-1)2+2=2i2-2i+3
∴A(i,3)=2A(i,2)(i≥2);即②正确;
③[A(i,i)]2=(a(i-1)2+i)2=(2i2-i+1)2
A(i,1)•A(i,2i-1)=2i2-2i+2•2i2=22(i2-i+1)=(2i2-i+1)2=[A(i,i)]2,即③正确;
④A(i+1,1)=ai2+1=2i2+1,A(i,1)•22i-1=2i2-2i+2•22i-1=2i2+1
∴A(i+1,1)=A(i,1)•22i-1,即④正确;
故答案为:①②③④.
点评:此题考查数列最一般的方法是观察法.
通过行数与项之间的关系可以找到规律,
题中还反映了从特殊到一般的数学思想.
通过行数与项之间的关系可以找到规律,
题中还反映了从特殊到一般的数学思想.

练习册系列答案
相关题目
 已知an=2n,把数列{an}各项按如图规律排成三角形数阵,记F(m,n)表示第m行从左至右的第n个数,则F(8,6)=
已知an=2n,把数列{an}各项按如图规律排成三角形数阵,记F(m,n)表示第m行从左至右的第n个数,则F(8,6)=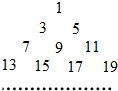 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 .
已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 . 已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 .
已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 . 已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 .
已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 .