题目内容
设圆C:(x-1)2+y2=1,过原点O作圆的任意弦,求所作弦的中点的轨迹方程.
解:

法一 :直接法.如图,设OQ为过O点的一条弦,P(x,y)为其中点,则CP⊥OQ.因OC中点为M
:直接法.如图,设OQ为过O点的一条弦,P(x,y)为其中点,则CP⊥OQ.因OC中点为M ,连接PM.
,连接PM.
故|MP|= |OC|=
|OC|= ,得方程
,得方程 2+y2=
2+y2= ,
,
由圆的范围知0<x≤1.
法二:定义法.∵∠OPC=90°,
∴动点P在以点M 为圆心,OC为直径的圆上,由圆的方程得
为圆心,OC为直径的圆上,由圆的方程得 2+y2=
2+y2= (0<x≤1).
(0<x≤1).
法三:代入法.设P(x,y),Q(x1,y1),则
 又∵(x1-1)2+y
又∵(x1-1)2+y =1,
=1,
∴(2x-1)2+(2y)2=1(0<x≤1).

练习册系列答案
相关题目
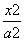 +
+ =1(a>b>0)的右焦点为F,过F的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,
=1(a>b>0)的右焦点为F,过F的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°, =2
=2 .
. C的离心率;
C的离心率;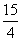 ,求椭圆C的方程.
,求椭圆C的方程. -
-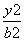 =1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )
=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( )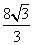 y B.x2=
y B.x2=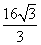 y
y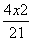 -
-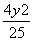 =1 B.
=1 B.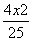 -
-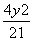 =1 D.
=1 D. (a>0),且满足条件sinC-sinB=
(a>0),且满足条件sinC-sinB= )在双曲线
)在双曲线 -
- =1上,则点P到该双曲线左焦点的距
=1上,则点P到该双曲线左焦点的距 离为________.
离为________. 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
, 成等差数列.
成等差数列. 的前
的前 ,则
,则 , , ,
, , ,
 和
和 有相同的解集,则不等式
有相同的解集,则不等式 的解集是( )
的解集是( ) C.
C. D.
D. 