题目内容
在△ABC中,2sinA+cosB=2,sinB+2cosA=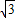 ,则∠C的大小应为( )
,则∠C的大小应为( )A.
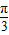
B.
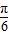
C.
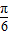 或
或 π
πD.
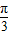 或
或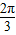
【答案】分析:先对条件中两个式子平方后相加得到关于A+B的正弦值,再由诱导公式得到角C的正弦值,最后得到答案.
解答:解:对2sinA+cosB=2,sinB+2cosA=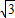 两边分别平方,
两边分别平方,
得:(2sinA+cosB)2=4,(sinB+2cosA)2=3,
两式相加化简得:4(sinAcosB+sinBcosA)=2,
整理得:sin(A+B)= ,
,
∴sin(180°-C)=sin(A+B)=sinC= ,
,
∴∠C=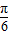 或
或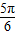 ,
,
若C=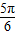 ,可得A+B=
,可得A+B=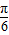 ,cosB<1,2sinA<1,2sinA+cosB=2,不成立,
,cosB<1,2sinA<1,2sinA+cosB=2,不成立,
所以C=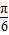 .
.
故选B
点评:此题考查了两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.
解答:解:对2sinA+cosB=2,sinB+2cosA=
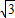 两边分别平方,
两边分别平方,得:(2sinA+cosB)2=4,(sinB+2cosA)2=3,
两式相加化简得:4(sinAcosB+sinBcosA)=2,
整理得:sin(A+B)=
 ,
,∴sin(180°-C)=sin(A+B)=sinC=
 ,
,∴∠C=
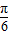 或
或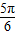 ,
,若C=
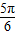 ,可得A+B=
,可得A+B=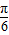 ,cosB<1,2sinA<1,2sinA+cosB=2,不成立,
,cosB<1,2sinA<1,2sinA+cosB=2,不成立,所以C=
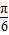 .
.故选B
点评:此题考查了两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目