题目内容
设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP,垂足为Po,且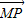 =
=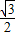
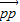 .
.(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设直线l:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
(1)若直线OA,AB,OB的斜率成等比数列,求实数m的取值范围;
(2)若以AB为直径的圆过曲线C与x轴正半轴的交点Q,求证:直线l过定点(Q点除外),并求出该定点的坐标.
【答案】分析:(Ⅰ)代入法:设点M(x,y),P(x,y),则由题意知P(x,0),由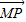 =
= 可得点M与点P坐标间的关系式,再根据点P在圆上代入P点坐标即可得到M坐标方程,即所求轨迹方程;
可得点M与点P坐标间的关系式,再根据点P在圆上代入P点坐标即可得到M坐标方程,即所求轨迹方程;
(Ⅱ)(1)设A(x1,y1),B(x2,y2),联立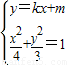 消掉y得x的二次方程,由题意知△>0①,根据直线OA,AB,OB的斜率成等比数列,得
消掉y得x的二次方程,由题意知△>0①,根据直线OA,AB,OB的斜率成等比数列,得 ,即
,即 ,借助韦达定理可得m、k的等式,进而求得k值,代入①即可解得m的范围;(2)依题意,
,借助韦达定理可得m、k的等式,进而求得k值,代入①即可解得m的范围;(2)依题意, ,即
,即 =0,变形为x1、x2的式子,进而用韦达定理可得k、m的等式,据m与k的关系式消掉直线l方程y=kx+m中的m,即可求得该直线所过定点;
=0,变形为x1、x2的式子,进而用韦达定理可得k、m的等式,据m与k的关系式消掉直线l方程y=kx+m中的m,即可求得该直线所过定点;
解答:解:(Ⅰ)设点M(x,y),P(x,y),则由题意知P(x,0).
由 ,
,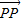 =(0,-y),且
=(0,-y),且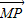 =
= ,得(x-x,-y)=
,得(x-x,-y)=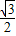 (0,-y).
(0,-y).
所以 ,于是
,于是 ,
,
又 ,所以
,所以 .
.
所以,点M的轨迹C的方程为 .
.
(Ⅱ)设A(x1,y1),B(x2,y2).
联立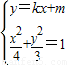 ,得(3+4k2)x2+8mkx+4(m2-3)=0.
,得(3+4k2)x2+8mkx+4(m2-3)=0.
所以,△=(8mk)2-16(3+4k2)(m2-3)>0,即3+4k2-m2>0.①,且 ,
,
(1)依题意,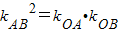 ,即
,即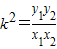 ,所以
,所以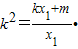
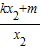 .
.
所以 =k2x1x2+km(x1+x2)+m2.
=k2x1x2+km(x1+x2)+m2.
所以km(x1+x2)+m2=0,即km(-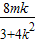 )+m2=0.
)+m2=0.
因为m≠0,所以k(- )+1=0,解得
)+1=0,解得 .
.
将得 代入①,得m2<6.
代入①,得m2<6.
所以,m的取值范围是(-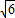 ,0)∪(0,
,0)∪(0, ).
).
(2)曲线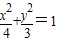 与x轴正半轴的交点为Q(2,0).
与x轴正半轴的交点为Q(2,0).
依题意, ,即
,即 =0.
=0.
于是(2-x1,-y1)•(2-x2,-y2)=0.
∴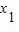 x2-2(x1+x2)+4+y1y2=0,即
x2-2(x1+x2)+4+y1y2=0,即 x2-2(x1+x2)+4+(kx1+m)(kx2+m)=0,
x2-2(x1+x2)+4+(kx1+m)(kx2+m)=0,
∴(k2+1)• +(km-2)•(-
+(km-2)•(-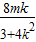 )+4+m2=0,
)+4+m2=0,
化简,得7m2+16mk+4k2=0.
解得,m=-2k或m=- ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,
当m=-2k时,直线l的方程为y=k(x-2),直线过定点(2,0)(舍去);
当m=- 时,直线l的方程为y=k(x-
时,直线l的方程为y=k(x- ),直线过定点(
),直线过定点( ,0).
,0).
所以,直线过定点( ,0).
,0).
点评:本题考查直线与圆锥曲线的位置关系、轨迹方程、直线斜率及等比数列等有关知识,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,难度较大.
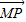 =
= 可得点M与点P坐标间的关系式,再根据点P在圆上代入P点坐标即可得到M坐标方程,即所求轨迹方程;
可得点M与点P坐标间的关系式,再根据点P在圆上代入P点坐标即可得到M坐标方程,即所求轨迹方程;(Ⅱ)(1)设A(x1,y1),B(x2,y2),联立
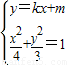 消掉y得x的二次方程,由题意知△>0①,根据直线OA,AB,OB的斜率成等比数列,得
消掉y得x的二次方程,由题意知△>0①,根据直线OA,AB,OB的斜率成等比数列,得 ,即
,即 ,借助韦达定理可得m、k的等式,进而求得k值,代入①即可解得m的范围;(2)依题意,
,借助韦达定理可得m、k的等式,进而求得k值,代入①即可解得m的范围;(2)依题意, ,即
,即 =0,变形为x1、x2的式子,进而用韦达定理可得k、m的等式,据m与k的关系式消掉直线l方程y=kx+m中的m,即可求得该直线所过定点;
=0,变形为x1、x2的式子,进而用韦达定理可得k、m的等式,据m与k的关系式消掉直线l方程y=kx+m中的m,即可求得该直线所过定点;解答:解:(Ⅰ)设点M(x,y),P(x,y),则由题意知P(x,0).
由
 ,
,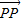 =(0,-y),且
=(0,-y),且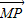 =
= ,得(x-x,-y)=
,得(x-x,-y)=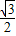 (0,-y).
(0,-y).所以
 ,于是
,于是 ,
,又
 ,所以
,所以 .
.所以,点M的轨迹C的方程为
 .
.(Ⅱ)设A(x1,y1),B(x2,y2).
联立
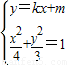 ,得(3+4k2)x2+8mkx+4(m2-3)=0.
,得(3+4k2)x2+8mkx+4(m2-3)=0.所以,△=(8mk)2-16(3+4k2)(m2-3)>0,即3+4k2-m2>0.①,且
 ,
,(1)依题意,
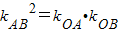 ,即
,即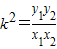 ,所以
,所以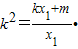
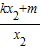 .
.所以
 =k2x1x2+km(x1+x2)+m2.
=k2x1x2+km(x1+x2)+m2.所以km(x1+x2)+m2=0,即km(-
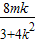 )+m2=0.
)+m2=0.因为m≠0,所以k(-
 )+1=0,解得
)+1=0,解得 .
.将得
 代入①,得m2<6.
代入①,得m2<6.所以,m的取值范围是(-
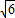 ,0)∪(0,
,0)∪(0, ).
).(2)曲线
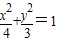 与x轴正半轴的交点为Q(2,0).
与x轴正半轴的交点为Q(2,0).依题意,
 ,即
,即 =0.
=0.于是(2-x1,-y1)•(2-x2,-y2)=0.
∴
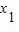 x2-2(x1+x2)+4+y1y2=0,即
x2-2(x1+x2)+4+y1y2=0,即 x2-2(x1+x2)+4+(kx1+m)(kx2+m)=0,
x2-2(x1+x2)+4+(kx1+m)(kx2+m)=0,∴(k2+1)•
 +(km-2)•(-
+(km-2)•(-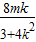 )+4+m2=0,
)+4+m2=0,化简,得7m2+16mk+4k2=0.
解得,m=-2k或m=-
 ,且均满足3+4k2-m2>0,
,且均满足3+4k2-m2>0,当m=-2k时,直线l的方程为y=k(x-2),直线过定点(2,0)(舍去);
当m=-
 时,直线l的方程为y=k(x-
时,直线l的方程为y=k(x- ),直线过定点(
),直线过定点( ,0).
,0).所以,直线过定点(
 ,0).
,0).点评:本题考查直线与圆锥曲线的位置关系、轨迹方程、直线斜率及等比数列等有关知识,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,难度较大.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
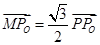 .
.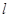 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.