题目内容
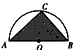
如图所示,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线![]() 与曲线C相交于不同的两点M、N,且M在D、N之间,设
与曲线C相交于不同的两点M、N,且M在D、N之间,设![]() ,求
,求![]() 的取值范围.
的取值范围.
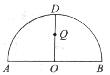
解:(1)分别以AB、OD所在直线为![]() 轴、
轴、![]() 轴,O为原点,建立平面直角坐标系,
轴,O为原点,建立平面直角坐标系,
∵|PA|+|PB|=|QA|+|QB|=2![]() .
.
∴曲线C为以原点为中心,A、B为焦点的椭圆.
设其长半轴为![]() ,短半轴为b,半焦距为c,则2
,短半轴为b,半焦距为c,则2![]() ,
,
∴![]() .
.![]() ,
,![]() ,∴曲线C的方程为
,∴曲线C的方程为![]() .
.
(2)当直线![]() 的斜率不存在时,可解得
的斜率不存在时,可解得![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
将点M(![]() ,
,![]() )、N(
)、N(![]() ,
,![]() )代入曲线方程
)代入曲线方程![]() ,
,
得(1+5![]() 2)
2)![]() 2+20
2+20![]()
![]() +15=0.
+15=0.
△=(20![]() )2―4×15(1+5
)2―4×15(1+5![]() 2)>0,得
2)>0,得![]() 2>
2>![]() .
.
![]() ,
,![]()
分析可知面![]() ,即
,即![]() ,
,

由式①②可得![]() ,∵
,∵![]() ,
,
∴![]() 即
即![]() .
.
∵在D与N之间,∴DM<DN,∴![]() ,即得
,即得![]()
综上所述,实数![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目

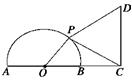 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以