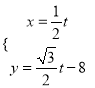题目内容
【题目】已知函数![]() 和
和![]() .
.
(1)讨论函数![]() 的奇偶性;
的奇偶性;
(2)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:
(1)首先确定函数的定义域为R,然后分类讨论可得当![]() 时,
时, ![]() 为偶函数;
为偶函数;
当![]() 时,
时, ![]() 既非奇函数又非偶函数;
既非奇函数又非偶函数;
(2)结合题意和二次函数的性质可得当![]() 时,
时, ![]() 的值域为
的值域为![]() ;当
;当![]() 时,
时, ![]() 的值域为
的值域为![]() .
.
试题解析:
(1)函数![]() ,其定义域为
,其定义域为![]() ,
,
1°当![]() 时,
时, ![]() ,∵
,∵![]() ,
,
∴![]() 为偶函数;
为偶函数;
2°当![]() 时,
时, ![]() ,取
,取![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() 且
且![]() ,∴
,∴![]() 既非奇函数又非偶函数;
既非奇函数又非偶函数;
(2)函数![]() ,其中
,其中![]() ,
,
设函数![]() ,其对称轴为
,其对称轴为![]() ,
, ![]() ,
, ![]() ,
,
1°当![]() ,即
,即![]() 时,
时, ![]() 对
对![]() 恒成立且在
恒成立且在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,
, ![]() ,
,
即![]() 的值域为
的值域为![]() ;
;
2°当![]() ,即
,即![]() 时,令
时,令![]() ,有
,有![]() (舍)和
(舍)和![]() ,
,
![]() 在
在![]() 上单调递增,且当
上单调递增,且当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,且
上递增,且![]() ,∴
,∴![]() ,
,
![]()
![]()
①当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 的值域为
的值域为![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 的值域为
的值域为![]() .
.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目