题目内容
【题目】已知函数![]() .
.
(1)当![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(2)方程![]() 在
在![]() 上的两解分别为
上的两解分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用三角恒等变换思想化简函数![]() 的解析式为
的解析式为![]() ,令
,令![]() ,可得
,可得![]() ,再令
,再令![]() ,可将问题转化为二次函数
,可将问题转化为二次函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,利用二次函数的基本性质可求出实数
,利用二次函数的基本性质可求出实数![]() 的值;
的值;
(2)设![]() ,由题意求得
,由题意求得![]() ,
,![]() ,
,![]() ,由两角差的余弦公式可求出
,由两角差的余弦公式可求出![]() 的值,求出
的值,求出![]() 的取值范围,进而利用二倍角余弦公式可求出
的取值范围,进而利用二倍角余弦公式可求出![]() 的值.
的值.
(1)![]()
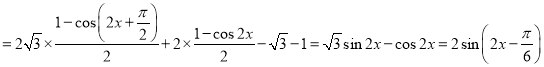 ,
,
当![]() 时,令
时,令![]() ,则
,则![]() ,则
,则![]() .
.
![]() ,
,
令![]() ,令
,令![]() ,该二次函数图象开口向上,对称轴为直线
,该二次函数图象开口向上,对称轴为直线![]() .
.
①当![]() 时,二次函数
时,二次函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() ,不合乎题意;
,不合乎题意;
②当![]() 时,二次函数
时,二次函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,则
上单调递减,则![]() ,解得
,解得![]() 或
或![]() (舍);
(舍);
③当![]() 时,二次函数
时,二次函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() ,解得
,解得![]() (舍).
(舍).
综上所述,![]() ;
;
(2)设![]() ,
,![]() ,则
,则![]() ,
,
由于正弦函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
由![]() ,得
,得![]() ,
,
因为方程![]() 在
在![]() 上的两解分别为
上的两解分别为![]() 、
、![]() ,
,
则![]() ,必有
,必有![]() ,
,![]() ,
,
所以,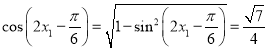 ,同理
,同理![]() ,
,
![]()
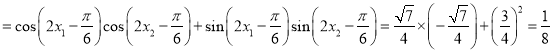 ,
,
由于![]() ,
,![]() 且
且![]() ,
,![]() ,则
,则![]() ,
,
由![]() ,可得
,可得![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目