题目内容
出定义在(0,+∞)上的三个函数:f(x)=lnx,g(x)=x2-af(x),h(x)=x-a
,已知g(x)在x=1处取极值.
(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当1<x<e2时,恒有x<
成立;
(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.
| x |
(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当1<x<e2时,恒有x<
| 2+f(x) |
| 2-f(x) |
(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.
分析:(Ⅰ)由题设,g(x)=x2-alnx,则g′(x)=2x-
.由已知,g'(1)=0,a=2.于是h(x)=x-2
,则h′(x)=1-
.由此能确定确定函数h(x)的单调性.
(Ⅱ)当1<x<e2时,0<lnx<2,即0<f(x)<2.欲证x<
,只需证x[2-f(x)]<2+f(x),即证f(x)>
.由此能够证明当1<x<e2时,恒有x<
成立.
(Ⅲ)由题设,h1(x)=x-2
+6.令g(x)-h1(x)=0,则2
-2lnx=-x2+x+6.设h2(x)=2
-2lnx,h3(x)=-x2+x+6(x>0),则h2′(x)=
-
=
,由
-2>0,得x>4.
所以h2(x)在(4,+∞)上是增函数,在(0,4)上是减函数.由此入手能够确定函数y=g(x)-h1(x)的零点个数.
| a |
| x |
| x |
| 1 | ||
|
(Ⅱ)当1<x<e2时,0<lnx<2,即0<f(x)<2.欲证x<
| 2+f(x) |
| 2-f(x) |
| 2(x-1) |
| x+1 |
| 2+f(x) |
| 2-f(x) |
(Ⅲ)由题设,h1(x)=x-2
| x |
| x |
| x |
| 1 | ||
|
| 2 |
| x |
| ||
| x |
| x |
所以h2(x)在(4,+∞)上是增函数,在(0,4)上是减函数.由此入手能够确定函数y=g(x)-h1(x)的零点个数.
解答:解:(Ⅰ)由题设,g(x)=x2-alnx,
则g′(x)=2x-
.(1分)
由已知,g'(1)=0,
即2-a=0⇒a=2.(2分)
于是h(x)=x-2
,
则h′(x)=1-
.(3分)
由h′(x)=1-
>0⇒x>1,
所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.(4分)
证明:(Ⅱ)当1<x<e2时,0<lnx<2,
即0<f(x)<2.(5分)
欲证x<
,
只需证x[2-f(x)]<2+f(x),
即证f(x)>
.(6分)
设φ(x)=f(x)-
=lnx-
,
则φ′(x)=
-
=
.
当1<x<e2时,φ'(x)>0,
所以φ(x)在区间(1,e2)上为增函数.(7分)
从而当1<x<e2时,φ(x)>φ(1)=0,
即lnx>
,
故x<
.(8分)
解:(Ⅲ)由题设,h1(x)=x-2
+6.
令g(x)-h1(x)=0,
则x2-2lnx-(x-2
+6)=0,
即2
-2lnx=-x2+x+6.(9分)
设h2(x)=2
-2lnx,
h3(x)=-x2+x+6(x>0),
则h2′(x)=
-
=
,
由
-2>0,得x>4.
所以h2(x)在(4,+∞)上是增函数,
在(0,4)上是减函数.(10分)
又h3(x)在(0,
)上是增函数,
在(
,+∞)上是减函数.
因为当x→0时,h2(x)→+∞,h3(x)→6.
又h2(1)=2,h3(1)=6,h2(4)=4-2ln4>0,h3(4)=-6,
则函数h2(x)与h3(x)的大致图象如下:(12分)

由图可知,当x>0时,两个函数图象有2个交点,
故函数y=g(x)-h1(x)有2个零点.(13分)
则g′(x)=2x-
| a |
| x |
由已知,g'(1)=0,
即2-a=0⇒a=2.(2分)
于是h(x)=x-2
| x |
则h′(x)=1-
| 1 | ||
|
由h′(x)=1-
| 1 | ||
|
所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.(4分)
证明:(Ⅱ)当1<x<e2时,0<lnx<2,
即0<f(x)<2.(5分)
欲证x<
| 2+f(x) |
| 2-f(x) |
只需证x[2-f(x)]<2+f(x),
即证f(x)>
| 2(x-1) |
| x+1 |
设φ(x)=f(x)-
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
则φ′(x)=
| 1 |
| x |
| 2(x+1)-2(x-1) |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
当1<x<e2时,φ'(x)>0,
所以φ(x)在区间(1,e2)上为增函数.(7分)
从而当1<x<e2时,φ(x)>φ(1)=0,
即lnx>
| 2(x-1) |
| x+1 |
故x<
| 2+f(x) |
| 2-f(x) |
解:(Ⅲ)由题设,h1(x)=x-2
| x |
令g(x)-h1(x)=0,
则x2-2lnx-(x-2
| x |
即2
| x |
设h2(x)=2
| x |
h3(x)=-x2+x+6(x>0),
则h2′(x)=
| 1 | ||
|
| 2 |
| x |
| ||
| x |
由
| x |
所以h2(x)在(4,+∞)上是增函数,
在(0,4)上是减函数.(10分)
又h3(x)在(0,
| 1 |
| 2 |
在(
| 1 |
| 2 |
因为当x→0时,h2(x)→+∞,h3(x)→6.
又h2(1)=2,h3(1)=6,h2(4)=4-2ln4>0,h3(4)=-6,
则函数h2(x)与h3(x)的大致图象如下:(12分)

由图可知,当x>0时,两个函数图象有2个交点,
故函数y=g(x)-h1(x)有2个零点.(13分)
点评:本题考函数的恒成立的应用,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.解题时要认真审题,注意导数的合理运用.

练习册系列答案
相关题目
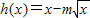 ,已知g(x)在x=1处取极值.
,已知g(x)在x=1处取极值.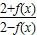 >x成立.
>x成立.