题目内容
给出定义在(0,+∞)上的三个函数:f(x)=lnx,g(x)=x2-af(x),h(x)=x-a
,已知g(x)在x=1处取极值.
(1)确定函数h(x)的单调性;
(2)求证:当1<x<e2时,恒有x<
成立.
| x |
(1)确定函数h(x)的单调性;
(2)求证:当1<x<e2时,恒有x<
| 2+f(x) |
| 2-f(x) |
分析:(1)由题设,知g(x)=x2-alnx,则g′(x)=2x-
.由g'(1)=0,知a=2于是h(x)=x-2
,由此能确定h(x)的单调性.
(2)当1<x<e2时,0<f(x)<2,所以 2-f(x)>0,欲证x<
,只需证x[2-f(x)]<2+f(x),即证f(x)>
.由此能够证明当1<x<e2时,x<
.
| a |
| x |
| x |
(2)当1<x<e2时,0<f(x)<2,所以 2-f(x)>0,欲证x<
| 2+f(x) |
| 2-f(x) |
| 2(x-1) |
| x+1 |
| 2+f(x) |
| 2-f(x) |
解答:解:(1)由题设,g(x)=x2-alnx,则g′(x)=2x-
.…(2分)
由已知,g'(1)=0,即2-a=0⇒a=2.…(3分)
于是h(x)=x-2
,则h′(x)=1-
.由h′(x)=1-
>0⇒x>1,…(5分)
所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.…(6分)
(2)当1<x<e2时,0<lnx<2,即0<f(x)<2,所以 2-f(x)>0…(8分)
欲证x<
,只需证x[2-f(x)]<2+f(x),即证f(x)>
.
设φ(x)=f(x)-
=lnx-
,
则φ′(x)=
-
=
.…(10分)
当1<x<e2时,φ'(x)>0,所以φ(x)在区间(1,e2)上为增函数.
从而当1<x<e2时,φ(x)>φ(1)=0,即lnx>
,故x<
.…(12分)
| a |
| x |
由已知,g'(1)=0,即2-a=0⇒a=2.…(3分)
于是h(x)=x-2
| x |
| 1 | ||
|
| 1 | ||
|
所以h(x)在(1,+∞)上是增函数,在(0,1)上是减函数.…(6分)
(2)当1<x<e2时,0<lnx<2,即0<f(x)<2,所以 2-f(x)>0…(8分)
欲证x<
| 2+f(x) |
| 2-f(x) |
| 2(x-1) |
| x+1 |
设φ(x)=f(x)-
| 2(x-1) |
| x+1 |
| 2(x-1) |
| x+1 |
则φ′(x)=
| 1 |
| x |
| 2(x+1)-2(x-1) |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
当1<x<e2时,φ'(x)>0,所以φ(x)在区间(1,e2)上为增函数.
从而当1<x<e2时,φ(x)>φ(1)=0,即lnx>
| 2(x-1) |
| x+1 |
| 2+f(x) |
| 2-f(x) |
点评:本题考查函数单调性的确定和不等式的证明,具体涉及到导数的性质和应用、函数的单调性、不等式的等价转化等基本知识.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
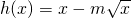 ,已知g(x)在x=1处取极值.
,已知g(x)在x=1处取极值.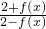 >x成立.
>x成立.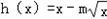 ,已知g(x)在x=1处取极值.
,已知g(x)在x=1处取极值.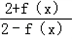 >x成立.
>x成立.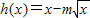 ,已知g(x)在x=1处取极值.
,已知g(x)在x=1处取极值.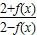 >x成立.
>x成立.